题目内容
5.已知数列{an}的前n项和为Sn,且Sn=n2+n(1)求数列{an}的通项公式;
(2)求数列{$\frac{{a}_{n}}{{2}^{n}}$}的前n项和为Tn.
分析 (1)当n≥2时,则an=Sn-Sn-1=2n,当n=1时,a1=S1=2,成立,即可求得求数列{an}的通项公式;
(2)由$\frac{{a}_{n}}{{2}^{n}}$=$\frac{2n}{{2}^{n}}$=$\frac{n}{{2}^{n-1}}$,利用“错位相减法”即可求得Tn.
解答 解:(1)由Sn=n2+n,
当n≥2时,则Sn-1=(n-1)2+(n-1),
则an=Sn-Sn-1=2n,
当n=1时,a1=S1=2,成立,
∴数列{an}的通项公式an=2n;
(2)由$\frac{{a}_{n}}{{2}^{n}}$=$\frac{2n}{{2}^{n}}$=$\frac{n}{{2}^{n-1}}$,
∴数列{$\frac{{a}_{n}}{{2}^{n}}$}的前n项和为Tn,Tn=$\frac{1}{{2}^{0}}$+$\frac{2}{2}$+$\frac{3}{{2}^{2}}$+…+$\frac{n}{{2}^{n-1}}$,
则$\frac{1}{2}$Tn=$\frac{1}{2}$+$\frac{2}{{2}^{2}}$+$\frac{3}{{2}^{3}}$+…+$\frac{n-1}{{2}^{n-1}}$+$\frac{n}{{2}^{n}}$,
两式相减得:$\frac{1}{2}$Tn=1+$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+…+$\frac{1}{{2}^{n-1}}$-$\frac{n}{{2}^{n}}$,
$\frac{1}{2}$Tn=1+$\frac{\frac{1}{2}-\frac{1}{{2}^{n-1}}×\frac{1}{2}}{1-\frac{1}{2}}$-$\frac{n}{{2}^{n}}$,
=$\frac{{2}^{n+1}-n-2}{{2}^{n}}$,
∴Tn=$\frac{{2}^{n+1}-n-2}{{2}^{n-1}}$,
数列{$\frac{{a}_{n}}{{2}^{n}}$}的前n项和为Tn,Tn=$\frac{{2}^{n+1}-n-2}{{2}^{n-1}}$.
点评 本题考查数列的通项公式的求法,考查“错位相减法”求数列的前n项和,考查计算能力,属于中档题.

 53天天练系列答案
53天天练系列答案| A. | -2 | B. | -i | C. | i | D. | -1 |
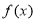 是定义在
是定义在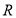 上的偶函数,且在区间
上的偶函数,且在区间 上单调递增,若实数
上单调递增,若实数 满足
满足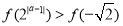 ,则
,则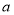 的取值范围是( )
的取值范围是( )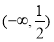 B.
B.
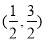 D.
D.
 的图象大致是( )
的图象大致是( ) B.
B. C.
C. D.
D.
 ,则
,则 ( )
( ) B.
B. C.
C. D.
D.
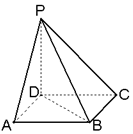 如图,已知ABCD是正方形,PD⊥平面ABCD,PD=AD.
如图,已知ABCD是正方形,PD⊥平面ABCD,PD=AD.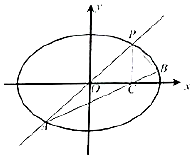 如图所示,已知椭圆$E:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$过点$({\sqrt{2},\sqrt{2}})$,直线l:y=kx(k≠0)与椭圆E交于P、A两点,过点P作PC⊥x轴,垂足为C点,直线AC交椭圆E与另一点B,当$k=\sqrt{2}$时,椭圆E的右焦点到直线l的距离为$\sqrt{2}$.
如图所示,已知椭圆$E:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$过点$({\sqrt{2},\sqrt{2}})$,直线l:y=kx(k≠0)与椭圆E交于P、A两点,过点P作PC⊥x轴,垂足为C点,直线AC交椭圆E与另一点B,当$k=\sqrt{2}$时,椭圆E的右焦点到直线l的距离为$\sqrt{2}$. 如图是甲、乙汽车4S店7个月销售汽车数量(单位:台)的茎叶图,若x是4与6的等差中项,y是2和8的等比中项,设甲店销售汽车的众数是a,乙店销售汽车中位数为b,则a+b的值为( )
如图是甲、乙汽车4S店7个月销售汽车数量(单位:台)的茎叶图,若x是4与6的等差中项,y是2和8的等比中项,设甲店销售汽车的众数是a,乙店销售汽车中位数为b,则a+b的值为( )