题目内容
15.同时具有性质“周期为π,图象关于直线x=$\frac{π}{3}$对称,在$[-\frac{π}{6},\frac{π}{3}]$上是增函数”的函数是( )| A. | $y=sin(\frac{x}{2}+\frac{π}{6})$ | B. | $y=cos(2x+\frac{π}{3})$ | C. | $y=cos(2x-\frac{π}{6})$ | D. | $y=sin(2x-\frac{π}{6})$ |
分析 根据函数周期性,对称性和单调性的性质进行判断即可.
解答 解:A.函数的周期T=$\frac{2π}{\frac{1}{2}}=4π$,不满足条件.
B.函数的周期T=π,当x=$\frac{π}{3}$时,y=sin($\frac{\frac{π}{3}}{2}$+$\frac{π}{6}$)=sin$\frac{π}{3}$≠±1,则函数关于x=$\frac{π}{3}$不对称,不满足条件.
C.函数的周期T=π,当x=$\frac{π}{3}$时,y=cos($\frac{2π}{3}$-$\frac{π}{6}$)=cos$\frac{π}{2}$=0,则函数关于($\frac{π}{3}$,0)对称,不满足条件.
D.函数的周期T=π,当x=$\frac{π}{3}$时,y=sin($\frac{2π}{3}$-$\frac{π}{6}$)=sin$\frac{π}{2}$=1,该函数关于关于直线x=$\frac{π}{3}$对称,在$[-\frac{π}{6},\frac{π}{3}]$上是增函数,满足条件.
故选:D.
点评 本题主要考查三角函数的性质,根据三角函数的周期性对称性和单调性的性质是解决本题的关键.

练习册系列答案
相关题目
5.已知函数f(x)=cosx+ax2-1,a∈R,若对于任意的实数x恒有f(x)≥0,则实数a的取值范围是( )
| A. | [$\frac{1}{2}$,+∞) | B. | ($\frac{1}{2}$,+∞) | C. | [-$\frac{1}{4}$,+∞) | D. | ($\frac{1}{4}$,+∞) |
3.已知全集为R,A=[1,+∞),B=(0,+∞),则(∁RA)∩B等于( )
| A. | (-∞,0) | B. | (0,1) | C. | (0,1] | D. | (1,+∞) |
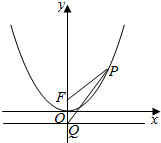 如图,设抛物线x2=4y的焦点为F,其准线与y轴相交于点Q,设P为抛物线上的一点,若$|{PQ}|=\sqrt{2}|{PF}|$,则△PQF的面积为2.
如图,设抛物线x2=4y的焦点为F,其准线与y轴相交于点Q,设P为抛物线上的一点,若$|{PQ}|=\sqrt{2}|{PF}|$,则△PQF的面积为2.