题目内容
20.函数f(x)=$\frac{x}{3}$+sinx的图象大致是( )| A. | 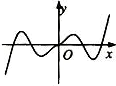 | B. | 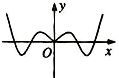 | C. | 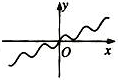 | D. | 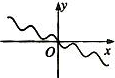 |
分析 判断函数的奇偶性,利用奇偶性的对称性进行判断,求函数的导数,利用导数研究函数的单调性和极值问题即可得到结论.
解答 解:∵f(-x)=-$\frac{x}{3}$-sinx)=-f(x),
∴f(x)是奇函数,则图象关于原点对称,排除B,
当x→+∞时,f(x)→+∞,当x→-∞时,f(x)→-∞,排除D,
函数的导数f′(x)=$\frac{1}{3}$+cosx,由f′(x)=$\frac{1}{3}$+cosx>0得cosx>-$\frac{1}{3}$,
在不等式cosx>-$\frac{1}{3}$的解的区间有无穷多个,即函数的单调递增区间有很多,排除A,
故选:C
点评 本题考查函数的图象,解题的关键是确定函数的单调性与奇偶性,利用函数的奇偶性和导数是解决本题的关键..

练习册系列答案
相关题目
10.设等差数列{an}的前n项和为Sn,若a1=1,S4=22,则S6=( )
| A. | 49 | B. | 51 | C. | 53 | D. | 55 |
8.当0<a<1时,不等式loga(4-x)>-log${\;}_{\frac{1}{a}}$x的解集是( )
| A. | (0,+∞) | B. | (0,2) | C. | (2,4) | D. | (0,4) |
15.同时具有性质“周期为π,图象关于直线x=$\frac{π}{3}$对称,在$[-\frac{π}{6},\frac{π}{3}]$上是增函数”的函数是( )
| A. | $y=sin(\frac{x}{2}+\frac{π}{6})$ | B. | $y=cos(2x+\frac{π}{3})$ | C. | $y=cos(2x-\frac{π}{6})$ | D. | $y=sin(2x-\frac{π}{6})$ |
 已知甲、乙两组数据如茎叶图所示,其中m∈(0,1,2,3,4,5,6,7,8,9),则甲的平均数不小于乙的平均数的概率为$\frac{3}{10}$.
已知甲、乙两组数据如茎叶图所示,其中m∈(0,1,2,3,4,5,6,7,8,9),则甲的平均数不小于乙的平均数的概率为$\frac{3}{10}$.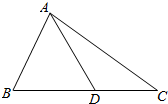 如图,锐角三角形ABC中,角A,B,C所对的边分别为a,b,c.若2bcosB=a•cosC+c•cosA
如图,锐角三角形ABC中,角A,B,C所对的边分别为a,b,c.若2bcosB=a•cosC+c•cosA