题目内容
7.设函数f(x)=sin(ωx-$\frac{3π}{4}$)(ω>0)的最小值正周期为π(1)求ω;
(2)若f($\frac{α}{2}$+$\frac{3π}{8}$)=$\frac{24}{25}$,且α∈(-$\frac{π}{2}$,$\frac{π}{2}$),求tanα的值.
分析 (1)由已知利用三角函数周期公式即可计算得解.
(2)由(1)可得:f(x)=sin(2x-$\frac{3π}{4}$),由已知可求sinα,利用同角三角函数基本关系式可求cosα,进而可求tanα=$\frac{sinα}{cosα}$的值.
解答 解:(1)∵f(x)=sin(ωx-$\frac{3π}{4}$)(ω>0)的最小值正周期为π,即:$\frac{2π}{ω}$=π,
∴ω=2,
(2)由(1)可得:f(x)=sin(2x-$\frac{3π}{4}$),
∴f($\frac{α}{2}$+$\frac{3π}{8}$)=sin[2($\frac{α}{2}$+$\frac{3π}{8}$)-$\frac{3π}{4}$]=sinα=$\frac{24}{25}$,
∵α∈(-$\frac{π}{2}$,$\frac{π}{2}$),
∴cosα=$\sqrt{1-si{n}^{2}α}$=$\frac{7}{25}$.
∴tanα=$\frac{sinα}{cosα}$=$\frac{24}{7}$.
点评 本题主要考查了三角函数周期公式,同角三角函数基本关系式的应用,考查了计算能力和转化思想,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7.若tan$\frac{π}{12}$cos$\frac{5π}{12}$=sin$\frac{5π}{12}$-msin$\frac{π}{12}$,则实数m的值为( )
| A. | 2$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 3 |
15.函数$y=sin\frac{1}{2}x$的最小正周期为( )
| A. | $\frac{π}{2}$ | B. | π | C. | 2π | D. | 4π |
2.如图,在平行四边形ABCD中,$\overrightarrow{AB}+\overrightarrow{AD}$=( )
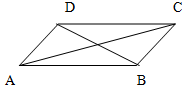

| A. | $\overrightarrow{AC}$ | B. | $\overrightarrow{CA}$ | C. | $\overrightarrow{BD}$ | D. | $\overrightarrow{DB}$ |
12.三个数a=0.412,b=log20.41,c=20.41之间的大小关系为( )
| A. | a<c<b | B. | a<b<c | C. | b<c<a | D. | b<a<c |
16.将函数y=cos(2x+$\frac{π}{4}$)的图象沿x轴向右平移φ(φ>0)个单位,得到一个偶函数的图象,则φ的一个可能取值为( )
| A. | $\frac{π}{16}$ | B. | $\frac{π}{8}$ | C. | $\frac{π}{4}$ | D. | $\frac{3π}{8}$ |
17.命题“?x≥0且x∈R,2x>x2”的否定是( )
| A. | ?x0≥0且x0∈R,${2^{x_0}}>{x_0}^2$ | B. | ?x≥0且x∈R,2x≤x2 | ||
| C. | ?x0≥0且x0∈R,${2^{x_0}}≤{x_0}^2$ | D. | ?x0<0且x0∈R,${2^{x_0}}≤{x_0}^2$ |