题目内容

14．设函数f（x）=ex（sinx-cosx）（0≤x≤2015π）的极小值点的个数为（　　）
A．1007B．1008C．2015D．2016

分析 令f′（x）=0，即sinx=0，解得x=kπ，（k∈Z）．根据0≤x≤2015π，可得0≤kπ≤2015π，解出即可得出．

解答 解：f′（x）=ex（cosx+sinx）+ex（sinx-cosx）=2exsinx．
令f′（x）=0，即sinx=0，解得x=kπ，（k∈Z）．
∵0≤x≤2015π，∴0≤kπ≤2015π，∴0≤k≤2015，
∴k的取值为2016个．
因此函数f（x）=ex（sinx-cosx）（0≤x≤2015π）的极小值点的个数为2016．
故选：D．

点评 本题考查了利用导数研究函数的单调性极值、三角函数求值，考查了推理能力与计算能力，属于中档题．

练习册系列答案
相关题目
4．已知函数f（x）=ln$\sqrt{1+2x}$+mx．
（Ⅰ）若f（x）为定义域上的单调函数，求实数m的取值范围；
（Ⅱ）当m=0，且0≤b＜a≤1时，证明：$\frac{4}{3}$＜$\frac{f（a）-f（b）}{a-b}$＜2．
5．已知函数$f（x）=2sin（\frac{x}{2}+\frac{π}{3}），x∈R$．
（1）求它的周期；
（2）求f（x）最大值和此时相应的x的值；
（3）求f（x）的单调增区间．
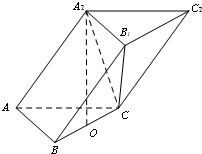2．在三棱柱ABC-A1B1C1中，已知AB=AC=AA1=$\sqrt{5}$，BC=4，BC的中点为O，A1O垂直于底面ABC．
（1）证明：在侧棱AA1上存在一点E，使得OE⊥平面BB1C1C，并求出AE的长；
（2）求二面角A1-B1C-B的平面角的余弦值．
9．已知F1（-2，0），F2（2，0）分别是椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左、右焦点，且椭圆C过点（-$\sqrt{3}$，1）．
（1）求椭圆C的方程；
（2）直线l过椭圆C的右焦点F2且斜率为1与椭圆C交于A，B两点，求弦AB的长；
（3）以第（2）题中的AB为边作一个等边三角形ABP，求点P的坐标．
19．已知函数$f（x）=sinx-\frac{1}{2}x$，x∈[0，π]．那么下列命题中所有真命题的序号是①④．
①f（x）的最大值是$f（\frac{π}{3}）$
②f（x）的最小值是$f（\frac{π}{3}）$
③f（x）在$[0，\frac{π}{3}]$上是减函数        
④f（x）在$[\frac{π}{3}，π]$上是减函数．
6．已知抛物线C：y2=2px（p＞0）的焦点为F（1，0）
（Ⅰ）求抛物线的方程；
（Ⅱ）已知过点（-1，0）的直线l与抛物线C交于A，B两点，且|FA|=2|FB|，求直线l的方程．
3．已知函数f（x）是定义在区间[-2，2]的奇函数，若f（x）+x•f′（x）＞0，则不等式（-x+1）•f（1-x）＞0的解集是[-1，1）．
4．已知f（x）=$\frac{{e}^{x}-1}{{e}^{x}+1}$（e为自然对数的底数）．
（1）求曲线y=f（x）在点（0，f（0））处的切线方程；
（2）求证：当x＞0时，f（x）＞$\frac{x}{x+2}$恒成立；
（3）已知k＞0，如果当x＞0时，f（x）＞$\frac{kx}{{e}^{x}+1}$恒成立，求k的最大值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网