题目内容
20.函数y=ax2+2x+1的图象与直线y=3x相切,则a=$\frac{1}{4}$.分析 设切点为(x0,y0),由于y′=2ax+2,利用导数的几何意义可得k=2ax0+2=3,又由于点(x0,y0)在曲线与直线上,可得y0=3x0,y0=ax02+2x0+1,即可解出a.
解答 解:设切点为(x0,y0),∵y′=2ax+2,∴k=2ax0+2=3,①
又∵点(x0,y0)在曲线与直线上,
∴y0=3x0,y0=ax02+2x0+1②
由①②得x0=2,a=$\frac{1}{4}$.
故答案为:$\frac{1}{4}$.
点评 熟练掌握导数的几何意义、切线的方程等是解题的关键.

练习册系列答案
相关题目
10.若f(x)为奇函数,且对任意实数x恒有f(x+3)-f(x-1)=0,则f(2)=( )
| A. | 0 | B. | -1 | C. | 1 | D. | 2 |
15.从4名男代表和2名女代表中选出3人参加座谈会,必须有女代表参加的不同选法共有( )种.
| A. | 12 | B. | 13 | C. | 16 | D. | 20 |
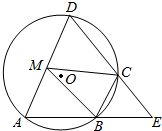 如图,四边形ABCD是⊙O的内接四边形,AB的延长线与DC的延长线交于点E,且CB=CE.
如图,四边形ABCD是⊙O的内接四边形,AB的延长线与DC的延长线交于点E,且CB=CE.