题目内容
13.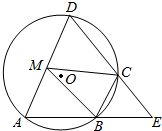 如图,四边形ABCD是⊙O的内接四边形,AB的延长线与DC的延长线交于点E,且CB=CE.
如图,四边形ABCD是⊙O的内接四边形,AB的延长线与DC的延长线交于点E,且CB=CE.(1)证明:∠D=∠E;
(2)设AD不是⊙O的直径,AD的中点为M,且MB=MC,证明:△ADE为等边三角形;
(3)若BC=1,且△ADE的外接圆半径为2,求四边形ABCD的面积.
分析 (1)利用四边形ABCD是⊙O的内接四边形,可得∠D=∠CBE,由CB=CE,可得∠E=∠CBE,可证明∠D=∠E;
(2)设BC的中点为N,连接MN,证明AD∥BC,可得∠A=∠CBE,进而得∠A=∠E,可证明△ADE为等边三角形;
(3)根据△ADE外接圆的半径求出高与边长,利用四边形ABCD是梯形,求出梯形的高h,即可计算梯形的面积.
解答 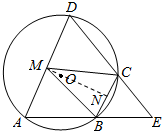 (1)证明:∵四边形ABCD是⊙O的内接四边形,
(1)证明:∵四边形ABCD是⊙O的内接四边形,
∴∠D=∠CBE,
∵CB=CE,
∴∠E=∠CBE,
∴∠D=∠E;
(2)证明:设BC的中点为N,连接MN,则由MB=MC知MN⊥BC,
∴O在直线MN上,
∵AD不是⊙O的直径,AD的中点为M,
∴OM⊥AD,
∴AD∥BC,
∴∠A=∠CBE,
∵∠CBE=∠E,
∴∠A=∠E,
由(1)知,∠D=∠E,
∴△ADE为等边三角形;
(3)△ADE是等边三角形,且外接圆的半径为2,
∴△ADE的高为3,
且$\frac{2}{3}$×$\frac{\sqrt{3}}{2}$AD=2,
∴AD=2$\sqrt{3}$;
又BC=1,BC∥AD,
∴四边形ABCD是梯形,设梯形的高为h,
则$\frac{3-h}{3}$=$\frac{1}{2\sqrt{3}}$,
解得h=$\frac{3(2\sqrt{3}-1)}{2\sqrt{3}}$;
∴梯形ABCD的面积为
S=$\frac{1}{2}$×(2$\sqrt{3}$+1)×$\frac{3(2\sqrt{3}-1)}{2\sqrt{3}}$=$\frac{11\sqrt{3}}{4}$.
点评 本题考查了圆的内接四边形性质,也考查了三角形外接圆以及求面积的应用问题,是综合性题目.

练习册系列答案
相关题目
2.将3个半径为1的球和一个半径为$\sqrt{2}-1$的球叠为两层放在桌面上,上层只放一个较小的球,四个球两两相切,那么上层小球的最高点到桌面的距离是( )
| A. | $\frac{{3\sqrt{2}+\sqrt{6}}}{3}$ | B. | $\frac{{\sqrt{3}+2\sqrt{6}}}{3}$ | C. | $\frac{{\sqrt{2}+2\sqrt{6}}}{3}$ | D. | $\frac{{2\sqrt{2}+\sqrt{6}}}{3}$ |
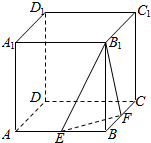 如图,在棱长为a的正方体ABCD-A1B1C1D1中,E、F分别是棱AB和BC的中点.
如图,在棱长为a的正方体ABCD-A1B1C1D1中,E、F分别是棱AB和BC的中点.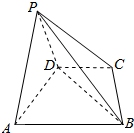 在四棱锥P-ABCD 中,△PAD 为等边三角形,底面ABCD为等腰梯形,满足AB∥CD,AD=DC=$\frac{1}{2}$AB=2,且平面PAD⊥平面ABCD.
在四棱锥P-ABCD 中,△PAD 为等边三角形,底面ABCD为等腰梯形,满足AB∥CD,AD=DC=$\frac{1}{2}$AB=2,且平面PAD⊥平面ABCD.