题目内容
8.从3件正品2件次品中任意抽取3件进行检查,则2件次品都被抽出的概率是$\frac{3}{10}$.分析 设三件正品为A,B,C,两件次品为a,b,任意抽取3件进行检查,一一列举出所有的基本事件,再找到满足条件的基本事件,根据概率公式计算即可.
解答 解:设三件正品为A,B,C,两件次品为a,b,任意抽取3件进行检查,共有(A,B,C),(A,B,a),(A,B,b),(A,C,a),(A,C,b),(A,a,b),(B,C,a),(B,C,b),(B,a,b),(C,a,b)共10种,其中2件次品都被抽出的有(A,a,b),(B,a,b),(C,a,b)共3种,
故2件次品都被抽出的概率是$\frac{3}{10}$,
故答案为:$\frac{3}{10}$.
点评 本题考查了古典概型概率的问题,关键是列举,属于基础题.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
16.已知数列{an}为等差数列,且a3+a5+a10+a12=64,则a7+a8=( )
| A. | 16 | B. | 64 | C. | 24 | D. | 32 |
13.已知直线1经过点(0,1)且与直线2x-y+3=0平行,则直线1的方程为( )
| A. | x+2y-2=0 | B. | x-2y+2=0 | C. | 2x-y+1=0 | D. | 2x-y-1=0 |
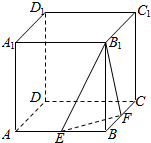 如图,在棱长为a的正方体ABCD-A1B1C1D1中,E、F分别是棱AB和BC的中点.
如图,在棱长为a的正方体ABCD-A1B1C1D1中,E、F分别是棱AB和BC的中点.