题目内容
已知函数f(x)=|2x-1|+ax.
(Ⅰ)当a=2时,解关于x的不等式f(x)≥|x-2|;
(Ⅱ)若f(x)≥x-
在R上恒成立,求实数a的取值范围.
(Ⅰ)当a=2时,解关于x的不等式f(x)≥|x-2|;
(Ⅱ)若f(x)≥x-
| 1 |
| 2 |
考点:绝对值不等式的解法
专题:不等式的解法及应用
分析:(Ⅰ)当a=2时,关于x的不等式即|2x-1|-|x-2|+2x≥0,转化为与之等价的三个不等式组,求出每个不等式组的解集,再取并集,即得所求.
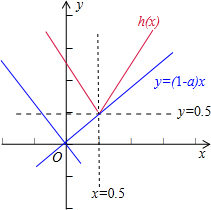
(Ⅱ)由题意可得函数h(x)=|2x-1|+
的图象应该在直线y=(1-a)x的上方或重合,可得0≤1-a≤2,或-2≤1-a<0,由此求得a的范围.
(Ⅱ)由题意可得函数h(x)=|2x-1|+
| 1 |
| 2 |
解答:
解:(Ⅰ)当a=2时,关于x的不等式f(x)≥|x-2|即|2x-1|+2x≥|x-2|,
即|2x-1|-|x-2|+2x≥0.
∴
①,或
②,或
.
解①求得x≥2,解②求得
≤x<2,解③求得x∈∅.
综上可得,不等式的解集为[
,+∞).
(Ⅱ)若f(x)≥x-
在R上恒成立,即|2x-1|+ax≥x-
在R上恒成立,
即|2x-1|+
≥(1-a)x.
故函数h(x)=|2x-1|+
的图象应该在直线y=(1-a)x的上方或重合.
如图所示:∴0≤1-a≤2,或-2≤1-a<0,解得-1≤a≤1,或 1<a≤3,
即a的范围是[-1,3].
即|2x-1|-|x-2|+2x≥0.
∴
|
|
|
解①求得x≥2,解②求得
| 3 |
| 5 |
综上可得,不等式的解集为[
| 3 |
| 5 |
(Ⅱ)若f(x)≥x-
| 1 |
| 2 |
| 1 |
| 2 |
即|2x-1|+
| 1 |
| 2 |
故函数h(x)=|2x-1|+
| 1 |
| 2 |
如图所示:∴0≤1-a≤2,或-2≤1-a<0,解得-1≤a≤1,或 1<a≤3,
即a的范围是[-1,3].

点评:本题主要考查绝对值不等式的解法,很熟的恒成立问题,体现了转化、分类讨论的数学思想,属于中档题.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目