题目内容
14.已知三棱锥P-ABC的体积为$\frac{8}{3},PA⊥$底面ABC,且△ABC的面积为4,三边AB,BC,CA的乘积为16,则三棱锥P-ABC的外接球的表面积为8π.分析 设△ABC外接圆半径为r,设三棱锥P-ABC球半径为R,由正弦定理,求出r=1,再由勾股定理得R=OP,由此能求出三棱锥的外接球的表面积.
解答 解:设△ABC的外接圆的半径为r,则S△ABC=$\frac{1}{2}absinC$=$\frac{1}{2}ab×\frac{c}{2r}=\frac{abc}{4r}$,解得r=1
∵三棱锥P-ABC的体积为$\frac{8}{3},PA⊥$底面ABC,且△ABC的面积为4.
∴$\frac{1}{3}×4×PA=\frac{8}{3}$,∴PA=2
如图,设球心为O,M为△ABC的外接圆的圆心,则OM=$\frac{1}{2}PA=1$
则三棱锥P-ABC的外接球的半径R=$\sqrt{O{M}^{2}+{r}^{2}}$=$\sqrt{2}$.
三棱锥P-ABC的外接球的表面积为4πR2=8π.
故答案为:8π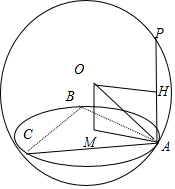
点评 本题考查三棱锥的外接球体积的求法,是中档题,解题时要认真审题,注意正弦定理、勾股定理的合理运用.属于中档题.

练习册系列答案
相关题目
5.已知sin(α+$\frac{π}{6}$)=-$\frac{1}{3}$,则sin(2α-$\frac{π}{6}$)的值为( )
| A. | $\frac{7}{9}$ | B. | -$\frac{7}{9}$ | C. | ±$\frac{2\sqrt{2}}{3}$ | D. | -$\frac{2}{3}$ |
2.一个六面体的三视图如图所示,其侧视图是边长为2的正方形,则该六面体的表面积是( )


| A. | $18+2\sqrt{5}$ | B. | $16+2\sqrt{5}$ | C. | $14+2\sqrt{5}$ | D. | $12+2\sqrt{5}$ |
9. 已知某几何体的三视图如图所示,则该几何体的体积为( )
已知某几何体的三视图如图所示,则该几何体的体积为( )
 已知某几何体的三视图如图所示,则该几何体的体积为( )
已知某几何体的三视图如图所示,则该几何体的体积为( )| A. | 216-20π | B. | 216-26π | C. | 216-60π | D. | 216-54π |
19.若△ABC的内角A,B,C的对边分别为a,b,c,且acosA=bcosB,则( )
| A. | △ABC为等腰三角形 | B. | △ABC为等腰三角形或直角三角形 | ||
| C. | △ABC为等腰直角三角形 | D. | △ABC为直角三角形 |
3.某公司奖励甲,乙,丙三个团队去A,B,C三个景点游玩,三个团队各去一个不同景点,征求三个团队意见得到:甲团队不去A;乙团队不去B;丙团队只去A或C.公司按征求意见安排,则下列说法一定正确的是( )
| A. | 丙团队一定去A景点 | B. | 乙团队一定去C景点 | ||
| C. | 甲团队一定去B景点 | D. | 乙团队一定去A景点 |
4.将半径为R的半圆卷成一个圆锥,圆锥的体积为( )
| A. | $\frac{\sqrt{3}}{3}$πR3 | B. | $\frac{\sqrt{3}}{6}$πR3 | C. | $\frac{1}{6}$πR3 | D. | $\frac{\sqrt{3}}{24}$πR3 |