题目内容
已知函数f(x)=
的定义域为R,则实数k的取值范围为 .
| 1 | ||
|
考点:函数的定义域及其求法
专题:函数的性质及应用
分析:根据函数的定义域为R,转化为不等式进行求解.
解答:
解:∵函数f(x)=
的定义域为R,
∴等价为kx2+kx+1>0恒成立,
若k=0,则不等式等价为1>0,成立,
若k≠0,要使不等式恒成立,
则满足
,
即
,
解得0<k<4,
综上0≤k<4,
故答案为:[0,4)
| 1 | ||
|
∴等价为kx2+kx+1>0恒成立,
若k=0,则不等式等价为1>0,成立,
若k≠0,要使不等式恒成立,
则满足
|
即
|
解得0<k<4,
综上0≤k<4,
故答案为:[0,4)
点评:本题主要考查函数恒成立问题,根据定义域为R转化为不等式恒成立是解决本题的关键.

练习册系列答案
相关题目
阅读如图所示的程序框图,运行相应的程序,若输出的结果是24,则判断框中应填入的内容为( )


| A、n≤3? | B、n≤4? |
| C、n≤5? | D、n≤6? |
复数-
的共轭复数是( )
| 1+i |
| i |
| A、1-i | B、-1+i |
| C、1+i | D、-1-i |
设全集U={1,2,3,4,5,6,7,8},A={1,2,3},B={3,4,5,6},则A∩(∁UB)=( )
| A、{1,2,3} |
| B、{1,2} |
| C、{1,3} |
| D、{1} |
过抛物线y2=4x(p>0)的焦点作两条互相垂直的弦AB、CD,则
+
=( )
| 1 |
| |AB| |
| 1 |
| |CD| |
| A、2 | ||
| B、4 | ||
C、
| ||
D、
|
 由正整点坐标(横坐标和纵坐标都是正整数)表示的一组平面向量
由正整点坐标(横坐标和纵坐标都是正整数)表示的一组平面向量| ai |
| am |
| am |
|
| a1 |
| a2 |
| a3 |
| a4 |
| a2015 |
| A、(44,11) |
| B、(44,10) |
| C、(45,11) |
| D、(45,10) |
已知底面边长为2cm,侧棱长为2
cm的正四棱柱各顶点都在同一球面上,则该球的体积为( )
| 3 |
A、
| ||||
B、5
| ||||
C、
| ||||
D、5
|
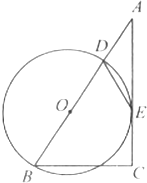 如图,在Rt△ABC中,∠A=30°,∠C=90°,D是AB边上的一点,以BD为直径的⊙O与AC相切于点E.若BC=6,则DE的长为
如图,在Rt△ABC中,∠A=30°,∠C=90°,D是AB边上的一点,以BD为直径的⊙O与AC相切于点E.若BC=6,则DE的长为