题目内容
在平面直角坐标系中,以坐标原点为极点,x轴的非负半轴为极轴建立极坐标系.已知点A的极坐标为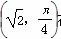 ,直线l的极坐标方程为ρcos
,直线l的极坐标方程为ρcos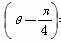 =a,且点A在直线l上.
=a,且点A在直线l上.
(1)求a的值及直线l的直角坐标方程;
(2)圆C的参数方程为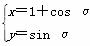 (α为参数),试判断直线l与圆C的位置关系.
(α为参数),试判断直线l与圆C的位置关系.
解:(1)由点A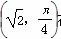 在直线ρcos
在直线ρcos 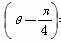 =a上,可得a=
=a上,可得a= .
.
所以直线l的方程可化为ρcos θ+ρsin θ=2,
从而直线l的直角坐标方程为x+y-2=0.
(2)由已知得圆C的直角坐标方程为(x-1)2+y2=1,
所以圆C的圆心为(1,0),半径r=1,
因为圆心C到直线l的距离d=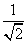 =
=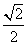 <1,所以直线l与圆C相交.
<1,所以直线l与圆C相交.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
马老师从课本上抄录一个随机变量ξ的概率分布列如下表:
| x | 1 | 2 | 3 |
| P(ξ=x) | ? | ! | ? |
请小牛同学计算ξ的数学期望.尽管“!”处完全无法看清,且两个“?”处字迹模糊,但能断定这两个“?”处的数值相同,据此,小牛给出了正确答案E(ξ)=________.
某学校为响应省政府号召,每学期派老师到各个民工子弟学校支教,以下是该学校50名老师上学期在某一个民工子弟学校支教的次数统计结果:
| 支教次数 | 0 | 1 | 2 | 3 |
| 人数 | 5 | 10 | 20 | 15 |
根据上表信息解答以下问题:
(1)从该学校任选两名老师,用η表示这两人支教次数之和,记“函数f(x)=x2-ηx-1在区间(4,5)上有且只有一个零点”为事件A,求事件A发生的概率P1;
(2)从该学校任选两名老师,用ξ表示这两人支教次数之差的绝对值,求随机变量ξ的分布列及数学期望E(ξ).
 、圆心角为60°的扇形的
、圆心角为60°的扇形的 弧上任取一点
弧上任取一点 ,作扇形的内接矩形
,作扇形的内接矩形 ,使点
,使点 在
在 上,点
上,点 在
在 上,设矩形
上,设矩形 .
. ,将
,将 的函数关系式;
的函数关系式; ,将
,将 的函数关系式.
的函数关系式.
 ,则函数
,则函数 的最小值为 .
的最小值为 .
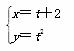 (t为参数),若l与C相交于A、B两点,则|AB|=________.
(t为参数),若l与C相交于A、B两点,则|AB|=________. (t为参数),P、Q分别为直线l与x轴、y轴的交点,线段PQ的中点为M.
(t为参数),P、Q分别为直线l与x轴、y轴的交点,线段PQ的中点为M. 的焦点到准线的距离是( )
的焦点到准线的距离是( ) D.
D.