题目内容
14.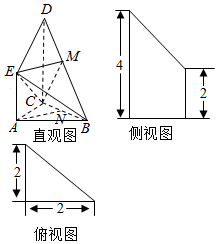 如图是某直三棱柱(侧棱与底面垂直)被削去上底后的直观图与三视图中的侧视图、俯视图,在直观图中,M是BD的中点,侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
如图是某直三棱柱(侧棱与底面垂直)被削去上底后的直观图与三视图中的侧视图、俯视图,在直观图中,M是BD的中点,侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.(1)若N是BC的中点,证明:AN∥平面CME;
(2)证明:平面BDE⊥平面BCD.
(3)求三棱锥D-BCE的体积.
分析 (1)连接MN,则MN$\stackrel{∥}{=}$$\frac{1}{2}$CD,由侧视图可知AE$\stackrel{∥}{=}$$\frac{1}{2}$CD,故MN$\stackrel{∥}{=}$AE,于是四边形ANME为平行四边形,得出AN∥EM,于是AN∥平面BDE;
(2)由AB=AC可得AN⊥BC,由侧面BCD⊥底面ABC可得AN⊥平面BCD,故而EM⊥平面BCD,于是平面BDE⊥平面BCD;
(3)以平面BCD为棱锥的底面,则EM为棱锥的高,利用直棱柱的结构特征计算棱锥的底面积和高,得出体积.
解答  (1)证明:连接MN,则MN是△BCD的中位线,∴MN∥CD,MN=$\frac{1}{2}$CD.
(1)证明:连接MN,则MN是△BCD的中位线,∴MN∥CD,MN=$\frac{1}{2}$CD.
由侧视图可知AE∥CD,AE=$\frac{1}{2}$CD,
∴MN=AE,MN∥AE
∴四边形ANME为平行四边形,
∴AN∥EM.∵AN?平面CME,EM?平面CME,
∴AN∥平面CME.
(2)证明:由俯视图可知AC=AB,∵N是BC的中点,
∴AN⊥BC,又平面ABC⊥平面BCD,平面ABC∩平面BCD=BC,AN?平面ABC,
∴AN⊥平面BCD.由(1)知AN∥EM,
∴EM⊥平面BCD.又EM?平面BDE,
∴平面BDE⊥平面BCD.
(3)解:由俯视图得AB⊥AC,AB=AC=2,
∴BC=$\sqrt{2}$AB=2$\sqrt{2}$,
∵N是BC中点,∴AN=$\frac{1}{2}BC=\sqrt{2}$,∴EM=$\sqrt{2}$.
由侧视图可知CD=4,CD⊥BC,
∴S△BCD=$\frac{1}{2}BC•CD$=$\frac{1}{2}×2\sqrt{2}×4$=4$\sqrt{2}$.
∴VD-BCE=VE-BCD=$\frac{1}{3}$S△BCD•|EM|=$\frac{1}{3}$×4$\sqrt{2}$×$\sqrt{2}$=$\frac{8}{3}$.
点评 本题考查了线面平行的判定,面面垂直的性质与判定,棱锥的体积计算,属于中档题.

| A. | (3,1)(-2,1) | B. | (0,1)(1,1) | C. | (1,0)(-1,0) | D. | (1,2)(-1,2) |
| A. | [3-2ln2,2) | B. | [3-2ln2,2] | C. | [e-1,2] | D. | [e-1,2) |