题目内容
19.已知O为原点,抛物线y=3-x2(y≥0)和平行于x轴的直线交于不同两点A、B,那么当△ABO的面积达到最大值时,A、B的坐标分别为( )| A. | (3,1)(-2,1) | B. | (0,1)(1,1) | C. | (1,0)(-1,0) | D. | (1,2)(-1,2) |
分析 可作出图形,并设平行于x轴的直线为y=m,(0<m<3),从而可得出$AB=2\sqrt{3-m}$,这样即可求得${S}_{△ABO}=\sqrt{3-m}•m$,可设$f(m)=\sqrt{3-m}•m(0<m<3)$,根据导数即可得出m=2时f(m)取到最大值,即△ABO的面积达到最大值,从而便可得出A,B两点的坐标.
解答 解:如图,设平行于x轴的直线方程为y=m(0<m<3),带入y=3-x2得,$x=±\sqrt{3-m}$;
∴$AB=2\sqrt{3-m}$;
∴${S}_{△ABO}=\sqrt{3-m}•m$;
设$f(m)=\sqrt{3-m}•m$,$f′(m)=\frac{3(2-m)}{2\sqrt{3-m}}$,0<m<3;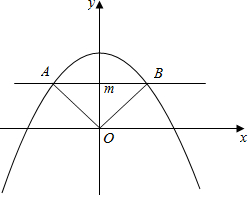
∴0<m<2时,f′(m)>0,2<m<3时,f′(m)<0;
∴m=2时,f(m)取得最大值2;
即此时△ABO的面积达到最大值;
∴此时A,B点的坐标分别为(-1,2),(1,2).
故选D.
点评 考查直线和曲线交点的坐标与直线方程和曲线方程形成方程组解的关系,二次函数图象的平移变换,三角形的面积公式,以及根据函数导数符号判断函数取得最值的方法,注意正确求导.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
9.下列函数中,既是偶函数又在(0,+∞)上单调递增的函数是( )
| A. | y=x3 | B. | y=|x+1| | C. | y=-x2 | D. | y=|x|+1 |
4.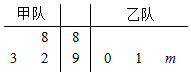 如图茎叶图表示的是甲乙两个篮球队在3次不同比赛中的得分情况,其中有一个数字模糊不清,在图中以m表示,若甲队的平均得分不低于乙队的平均得分,那么m的可能取值集合为( )
如图茎叶图表示的是甲乙两个篮球队在3次不同比赛中的得分情况,其中有一个数字模糊不清,在图中以m表示,若甲队的平均得分不低于乙队的平均得分,那么m的可能取值集合为( )
 如图茎叶图表示的是甲乙两个篮球队在3次不同比赛中的得分情况,其中有一个数字模糊不清,在图中以m表示,若甲队的平均得分不低于乙队的平均得分,那么m的可能取值集合为( )
如图茎叶图表示的是甲乙两个篮球队在3次不同比赛中的得分情况,其中有一个数字模糊不清,在图中以m表示,若甲队的平均得分不低于乙队的平均得分,那么m的可能取值集合为( )| A. | {2} | B. | {1,2} | C. | {0,1,2} | D. | {2,3} |
11.命题p:?φ∈R,函数f(x)=sin(2x+φ)不是偶函数,则¬p为( )
| A. | ?φ∈R,函数f(x)=sin(2x+φ)是奇函数 | B. | ?φ∈R,函数f(x)=sin(2x+φ)不是偶函数 | ||
| C. | ?φ∈R,函数f(x)=sin(2x+φ)是偶函数 | D. | ?φ∈R,函数f(x)=sin(2x+φ)是偶函数 |
8.执行如图所示的程序框图,若要使输出的y的值等于3,则输入的x的值可以是( )
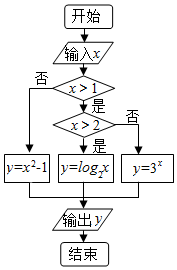

| A. | 1 | B. | 2 | C. | 8 | D. | 9 |
9.按如下程序框图,若输出的结果为170,试判断框内应补充的条件为( )

| A. | i>9 | B. | i≥9 | C. | i>11 | D. | i≥11 |
 如图(1),在Rt△ABC中,∠C=90°,BC=3,AC=6,D,E分别是AC,AB上的点,且DE∥BC,DE=2,将△ADE沿DE折起到△A1DE的位置,使A1C⊥CD,如图(2).
如图(1),在Rt△ABC中,∠C=90°,BC=3,AC=6,D,E分别是AC,AB上的点,且DE∥BC,DE=2,将△ADE沿DE折起到△A1DE的位置,使A1C⊥CD,如图(2).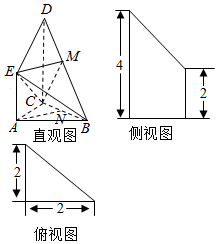 如图是某直三棱柱(侧棱与底面垂直)被削去上底后的直观图与三视图中的侧视图、俯视图,在直观图中,M是BD的中点,侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
如图是某直三棱柱(侧棱与底面垂直)被削去上底后的直观图与三视图中的侧视图、俯视图,在直观图中,M是BD的中点,侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.