题目内容
2．已知f（x）=m（x-m）（x+m+3）在区间[1，+∞）上的值恒为负数，且在区间（-∞，-4）上存在x0使得f（x0）＞0，求实数m的取值范围．分析 根据二次函数的表达式和二次函数图象的性质可知函数图象开口向下，且一根小于-4和一根小于1，分类解决即可．
解答 解：在区间[1，+∞）上的值恒为负数，
开口方向应向下，
∴m＜0，
函数的零点为2m，-m-3，
当2m＞-m-3时，
只需2m＜1，且-m-3＜-4，
解得无解；
当2m＜-m-3时，
只需2m＜-4，且-m-3＜1，
解得-4＜m＜-2．
故m的范围为-4＜m＜-2．
点评 考查了二次函数图象的性质和二次函数参数分类讨论．
练习册系列答案
相关题目
函数f（x）=2sin（ωx+φ）（ω＞0，-$\frac{π}{2}$＜φ＜$\frac{π}{2}$）的部分图象如图所示，则函数f（x）解析式f（x）=2sin（2x-$\frac{π}{3}$）．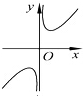
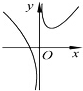
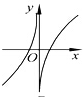
如图（1），在Rt△ABC中，∠C=90°，BC=3，AC=6，D，E分别是AC，AB上的点，且DE∥BC，DE=2，将△ADE沿DE折起到△A1DE的位置，使A1C⊥CD，如图（2）．
如图，在四棱锥S-ABCD中，已知底面ABCD为直角梯形，其中AD∥BC，∠BAD=90°，SA⊥底面ABCD，$SA=AB=BC=2，tan∠SDA=\frac{2}{3}$．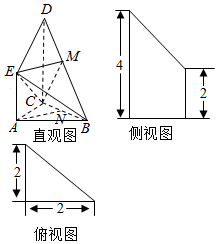
如图是某直三棱柱（侧棱与底面垂直）被削去上底后的直观图与三视图中的侧视图、俯视图，在直观图中，M是BD的中点，侧视图是直角梯形，俯视图是等腰直角三角形，有关数据如图所示．
11．命题p：?φ∈R，函数f（x）=sin（2x+φ）不是偶函数，则￢p为（ ）
| A． | ?φ∈R，函数f（x）=sin（2x+φ）是奇函数 | B． | ?φ∈R，函数f（x）=sin（2x+φ）不是偶函数 | ||
| C． | ?φ∈R，函数f（x）=sin（2x+φ）是偶函数 | D． | ?φ∈R，函数f（x）=sin（2x+φ）是偶函数 |