题目内容
已知a为常数,函数f(x)=x(lnx-ax)有两个极值点x1,x2(x1<x2),则( )
A.f(x1)>0,f(x2)>- B.f(x1)<0,f(x2)<-
B.f(x1)<0,f(x2)<-
C.f(x1)>0,f(x2)<- D.f(x1)<0,f(x2)>-
D.f(x1)<0,f(x2)>-
D
[解析] 由题意知,函数f(x)=x(lnx-ax)=xlnx-ax2有两个极值点,
即f ′(x)=lnx+1-2ax=0在区间(0,+∞)上有两个根.
令h(x)=lnx+1-2ax,则h′(x)=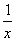 -2a=
-2a=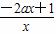 ,当a≤0时h′(x)>0,h(x)在区间(0,+∞)上递增,f ′(x)=0不可能有两个正根,
,当a≤0时h′(x)>0,h(x)在区间(0,+∞)上递增,f ′(x)=0不可能有两个正根,
∴a>0.由h′(x)=0,可得x=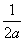 ,从而可知h(x)在区间(0,
,从而可知h(x)在区间(0,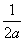 )上递增,在区间(
)上递增,在区间(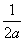 ,+∞)上递减.因此需h(
,+∞)上递减.因此需h(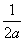 )=ln
)=ln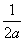 +1-1=ln
+1-1=ln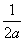 >0,即
>0,即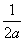 >1时满足条件,故当0<a<
>1时满足条件,故当0<a< 时,h(x)=0有两个根x1,x2,且x1<
时,h(x)=0有两个根x1,x2,且x1<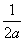 <x2.
<x2.
又h(1)=1-2a>0,∴x1<1<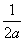 <x2,从而可知函数f(x)在区间(0,x1)上递减,在区间(x1,x2)上递增,在区间(x2,+∞)上递减.
<x2,从而可知函数f(x)在区间(0,x1)上递减,在区间(x1,x2)上递增,在区间(x2,+∞)上递减.
∴f(x1)<f(1)=-a<0,f(x2)>f(1)=-a>- .故选D.
.故选D.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
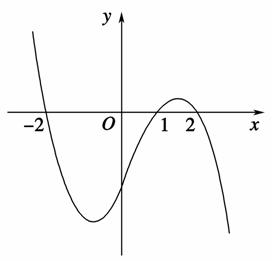
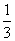 x3-
x3-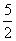 在区间[1,4]上存在次不动点,则实数a的取值范围是( )
在区间[1,4]上存在次不动点,则实数a的取值范围是( )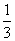 x3-
x3-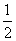 x2+3x-
x2+3x-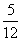 ,根据这一发现可得:
,根据这一发现可得: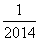 )+f(
)+f(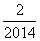 )+f(
)+f(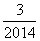 )+f(
)+f(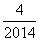 )+…+f(
)+…+f(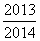 )=________.
)=________. 的函数
的函数 满足
满足 ,当
,当 时,
时, 若
若 时,
时, 恒成立,则实数
恒成立,则实数 的取值范围是
的取值范围是 B.
B. C.
C. D.
D.