题目内容
18.已知函数$f(x)=2sin\frac{πx}{4}$,如果存在实数x1,x2,使得对任意的实数x都有f(x1)≤f(x)≤f(x2),则|x1-x2|最小值是4.分析 f(x1),f(x2)分别是f(x)的最小值和最大值,|x1-x2|最小值即为f(x)的半周期.
解答 解:∵f(x1)≤f(x)≤f(x2),∴f(x1),f(x2)分别是f(x)的最小值和最大值,
∴|x1-x2|为f(x)的半周期.
∵f(x)的最小正周期T=$\frac{2π}{\frac{π}{4}}$=8,
∴|x1-x2|的最小值为4.
故答案为:4.
点评 本题考查了正弦函数的图象与性质,属于基础题.

练习册系列答案
相关题目
9.设a=30.5,b=log32,c=cos$\frac{2π}{3}$,则( )
| A. | a<b<c | B. | c<a<b | C. | b<c<a | D. | c<b<a |
13.设$a={π^{0.3}},b={log_π}3,c={log_3}sin\frac{2π}{3}$,则( )
| A. | a>b>c | B. | c>a>b | C. | b>a>c | D. | b>c>a |
3.若$cos(2π-α)=\frac{{-\sqrt{5}}}{3}$且$α∈(π,\frac{3π}{2})$,则sin(π+α)=( )
| A. | $-\frac{{\sqrt{5}}}{3}$ | B. | $-\frac{1}{3}$ | C. | $±\frac{2}{3}$ | D. | $\frac{2}{3}$ |
10.若z(1+i)=(1-i)2(i为虚数单位),则z=( )
| A. | 1+i | B. | 1-i | C. | -1+i | D. | -1-i |
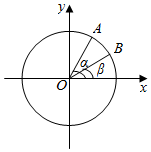 如图,在平面直角坐标系中xOy中,以Ox轴的非负半轴为始边做两个锐角α,β,它们的终边分别与单位圆相交于A、B两点,已知A,B的横坐标分别为$\frac{\sqrt{2}}{10}$,$\frac{2\sqrt{5}}{5}$.
如图,在平面直角坐标系中xOy中,以Ox轴的非负半轴为始边做两个锐角α,β,它们的终边分别与单位圆相交于A、B两点,已知A,B的横坐标分别为$\frac{\sqrt{2}}{10}$,$\frac{2\sqrt{5}}{5}$.