题目内容
8.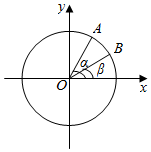 如图,在平面直角坐标系中xOy中,以Ox轴的非负半轴为始边做两个锐角α,β,它们的终边分别与单位圆相交于A、B两点,已知A,B的横坐标分别为$\frac{\sqrt{2}}{10}$,$\frac{2\sqrt{5}}{5}$.
如图,在平面直角坐标系中xOy中,以Ox轴的非负半轴为始边做两个锐角α,β,它们的终边分别与单位圆相交于A、B两点,已知A,B的横坐标分别为$\frac{\sqrt{2}}{10}$,$\frac{2\sqrt{5}}{5}$.(1)求cos,sinβ;
(2)若tanθ=cotβ,求$\frac{1}{3}$sinθcosθ+sin2θ+2的值.
分析 (1)在单位圆中,由已知点的横坐标求出纵坐标,利用三角函数的定义求得cosα,sinβ的值;
(2)由tanθ=cotβ求出tanθ,再把$\frac{1}{3}$sinθcosθ+sin2θ+2化弦为切得答案.
解答  解:(1)如图,在单位圆中,
解:(1)如图,在单位圆中,
∵A,B的横坐标分别为$\frac{\sqrt{2}}{10}$,$\frac{2\sqrt{5}}{5}$,
∴A的纵坐标为$\sqrt{1-(\frac{\sqrt{2}}{10})^{2}}=\frac{7\sqrt{2}}{10}$,B的纵坐标为$\sqrt{1-(\frac{2\sqrt{5}}{5})^{2}}=\frac{\sqrt{5}}{5}$.
∴cos$α=\frac{\sqrt{2}}{10}$,sin$β=\frac{\sqrt{5}}{5}$;
(2)tan$β=\frac{\frac{\sqrt{5}}{5}}{\frac{2\sqrt{5}}{5}}=\frac{1}{2}$,tanθ=cotβ=$\frac{1}{tanβ}=2$,
∴$\frac{1}{3}$sinθcosθ+sin2θ+2=$\frac{1}{3}$sinθcosθ+3sin2θ+2cos2θ
=$\frac{\frac{1}{3}sinθcosθ+3si{n}^{2}θ+2co{s}^{2}θ}{si{n}^{2}θ+co{s}^{2}θ}$=$\frac{\frac{1}{3}tanθ+3ta{n}^{2}θ+2}{ta{n}^{2}θ+1}$
=$\frac{\frac{1}{3}×2+3×4+2}{4+1}=\frac{\frac{44}{3}}{5}=\frac{44}{15}$.
点评 本题考查任意角的三角函数的定义,考查了三角函数的化简求值,对于(2)的求解,灵活利用sin2θ+cos2θ=1是关键,是中档题.

| A. | $\frac{7}{2}$ | B. | $\frac{5}{2}$ | C. | 3 | D. | 2 |
| A. | 1 | B. | 0 | C. | 2 | D. | -2 |
 如图,四边形ABCD是正方形,SA=SB=SC=SD,P是棱SC上的点,M,N分别是棱SB,SD上的点,SP:PC=1:2,SN:ND=2:1,SM:MB=2:1
如图,四边形ABCD是正方形,SA=SB=SC=SD,P是棱SC上的点,M,N分别是棱SB,SD上的点,SP:PC=1:2,SN:ND=2:1,SM:MB=2:1