题目内容
若（1+3x）n展开式各项系数和为256，设 i为虚数单位，复数（1+i）n的运算结果为
- A.4
- B.-4
- C.2
- D.-2
B
分析：根据（1+3x）n展开式各项系数和为256，求得 n=4，可得复数（1+i）n =（1+i）4=（2i）2，运算求得结果．
解答：在（1+3x）n展开式中，令x=1，可得（1+3x）n展开式各项系数和为 4n=256，∴n=4．
∴复数（1+i）n =（1+i）4=（2i）2=-4，
故选B．
点评：本题主要考查复数代数形式的乘方运算，二项式定理的应用，属于中档题．
分析：根据（1+3x）n展开式各项系数和为256，求得 n=4，可得复数（1+i）n =（1+i）4=（2i）2，运算求得结果．
解答：在（1+3x）n展开式中，令x=1，可得（1+3x）n展开式各项系数和为 4n=256，∴n=4．
∴复数（1+i）n =（1+i）4=（2i）2=-4，
故选B．
点评：本题主要考查复数代数形式的乘方运算，二项式定理的应用，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
=________．
”是“x=2kπ+
）（k∈Z）”成立的
=1（a＞0）与直线l：x+y=1相交于两个不同的点A、B．
．求a的值．
，则x+y=________．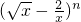 
的展开式的第5项是常数，则自然数n的值为