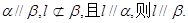题目内容
如图。在直三棱柱ABC—A1B1C1中,AB=BC=2AA1,∠ABC=90°,M是BC中点。

(I)求证:A1B∥平面AMC1;
(II)求直线CC1与平面AMC1所成角的正弦值;
(Ⅲ)试问:在棱A1B1上是否存在点N,使AN与MC1成角60°?若存在,确定点N的位置;若不存在,请说明理由。

(I)求证:A1B∥平面AMC1;
(II)求直线CC1与平面AMC1所成角的正弦值;
(Ⅲ)试问:在棱A1B1上是否存在点N,使AN与MC1成角60°?若存在,确定点N的位置;若不存在,请说明理由。
(I)由线线平行证得线面平行 (II)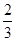 (Ⅲ)
(Ⅲ)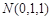 .在棱
.在棱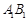 上存在棱
上存在棱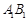 的中点
的中点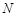 ,使
,使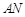 与
与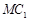 成角
成角 .
.
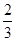 (Ⅲ)
(Ⅲ)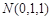 .在棱
.在棱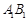 上存在棱
上存在棱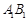 的中点
的中点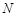 ,使
,使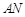 与
与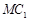 成角
成角 .
. 试题分析:(Ⅰ)连接
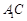 交
交 于
于 ,连接
,连接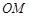 .在三角形
.在三角形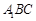 中,
中,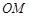 是三角形
是三角形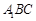 的中位线,
的中位线,所以
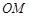 ∥
∥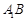 ,
,又因
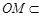 平面
平面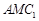 ,
,所以
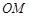 ∥平面
∥平面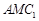 .
. (Ⅱ)(法一)设直线
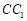 与平面
与平面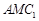 所成角为
所成角为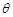 ,
,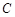 点到平面
点到平面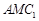 的距离为
的距离为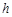
 ,不妨设
,不妨设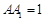 ,则
,则 ,
,因为
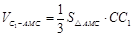 ,
,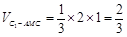 ,
,所以
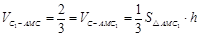 .
. 因为
 ,
,所以
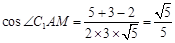 ,
,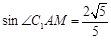 .
.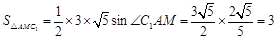 .
.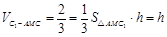 ,
,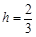 ,
,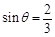 .
. (法二)如图以
 所在的直线为
所在的直线为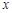 轴, 以
轴, 以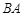 所在的直线为
所在的直线为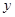 轴, 以
轴, 以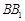 所在的直线为
所在的直线为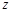 轴,以
轴,以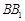 的长度为单位长度建立空间直角坐标系.
的长度为单位长度建立空间直角坐标系.
则
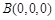 ,
,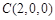 ,
,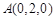 ,
,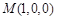 ,
,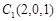 ,
,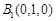 ,
,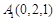 .设直线
.设直线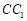 与平面
与平面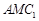 所成角为
所成角为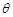 ,平面
,平面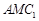 的法向量为
的法向量为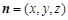 .则有
.则有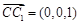 ,
,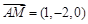 ,
,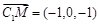 ,
,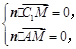
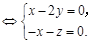 令
令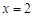 ,得
,得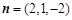 ,
,设直线
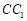 与平面
与平面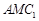 所成角为
所成角为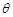 ,
,则
 .
. (Ⅲ)假设直线
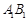 上存在点
上存在点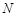 ,使
,使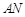 与
与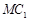 成角为
成角为 .
.设
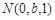 ,则
,则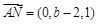 ,
,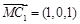 .
.设其夹角为
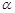 ,
,所以,
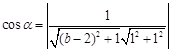
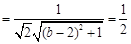 ,
,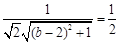 ,
,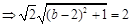
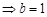 或
或 (舍去),
(舍去),故
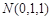 .所以在棱
.所以在棱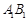 上存在棱
上存在棱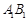 的中点
的中点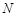 ,使
,使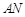 与
与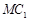 成角
成角 .
. 点评:此题考查直线与平面平行的判断及直线与平面垂直的判断,第一问此类问题一般先证明两个面平行,再证直线和面平行,这种做题思想要记住,此类立体几何题是每年高考必考的一道大题,难度比较大,计算要仔细.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
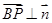 中,
中, ,
, ,
,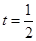 为
为 中点.(Ⅰ)证明:
中点.(Ⅰ)证明: ;(Ⅱ)求
;(Ⅱ)求 与平面
与平面 所成角的正弦值;(Ⅲ)在棱
所成角的正弦值;(Ⅲ)在棱 上是否存在一点
上是否存在一点 ,使得
,使得
 ,AF=1,M是线段EF的中点.
,AF=1,M是线段EF的中点.
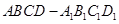 的底面是边长为1的正方形,侧棱垂直底边ABCD四棱柱,
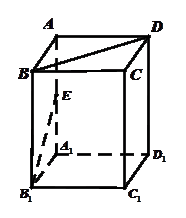
的底面是边长为1的正方形,侧棱垂直底边ABCD四棱柱,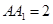 ,
,
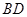 与B1E所成角的大小;
与B1E所成角的大小;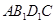 的体积.
的体积. 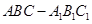 中,各棱长相等,侧棱垂直于底面,点
中,各棱长相等,侧棱垂直于底面,点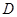 是侧面
是侧面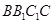 的中心,则
的中心,则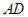 与平面
与平面
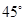
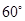
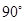
 ,E,F分别为AB、CB中点,过直线EF作棱柱的截面,若截面与平面ABC所成的二面角的大小为60º,则截面的面积为( ).
,E,F分别为AB、CB中点,过直线EF作棱柱的截面,若截面与平面ABC所成的二面角的大小为60º,则截面的面积为( ).
 中,
中, ,
, ,点
,点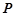 在
在 上,
上, 交
交 于
于 ,
, 交
交 于
于 .沿
.沿 将△
将△ 翻折成△
翻折成△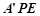 ,使平面
,使平面 平面
平面 将△
将△ 翻折成△
翻折成△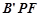 ,使平面
,使平面 平面
平面
 平面
平面 ,当
,当 为何值时,二面角
为何值时,二面角 的大小为
的大小为 ?
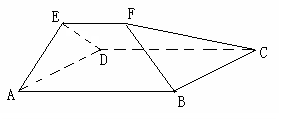
?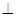 平面ABCD,EF∥AB, AB=2EF=2AD=4,
平面ABCD,EF∥AB, AB=2EF=2AD=4,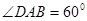 .
.
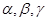 是三个不重合的平面,l是直线,给出下列命题:
是三个不重合的平面,l是直线,给出下列命题: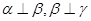 ,则
,则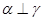 ; ②若
; ②若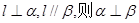
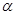 的距离相等,则
的距离相等,则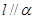 ; ④若
; ④若