题目内容
如图:在多面体EF-ABCD中,四边形ABCD是平行四边形,△EAD为正三角形,且平面EAD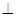 平面ABCD,EF∥AB, AB=2EF=2AD=4,
平面ABCD,EF∥AB, AB=2EF=2AD=4,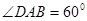 .
.
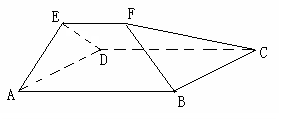
(Ⅰ)求多面体EF-ABCD的体积;
(Ⅱ)求直线BD与平面BCF所成角的大小.
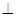 平面ABCD,EF∥AB, AB=2EF=2AD=4,
平面ABCD,EF∥AB, AB=2EF=2AD=4,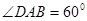 .
.
(Ⅰ)求多面体EF-ABCD的体积;
(Ⅱ)求直线BD与平面BCF所成角的大小.
(1)5(2)

试题分析:解(Ⅰ)如图.取AD的中点G,正△EAD中,
 ,又AD=2,故
,又AD=2,故  ,又因为平面EAD
,又因为平面EAD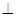 平面ABCD,所以
平面ABCD,所以 ,多面体EF-ABCD的体积
,多面体EF-ABCD的体积 ,而四边形ABCD的面积
,而四边形ABCD的面积 ,所以
,所以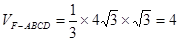 ;设AB的中点为H,因为AB=2EF,所以FH∥AE,所以
;设AB的中点为H,因为AB=2EF,所以FH∥AE,所以 ,所以
,所以 ,所以
,所以 ,故所求多面体EF-ABCD的体积是5
,故所求多面体EF-ABCD的体积是5
(Ⅱ)连接EH,由题设知EF=HB,又EF∥AB,所以四边形EHBF是平行四边形,连接GH,在△AGH中,AH=2AG=2,
 .故
.故 ,即
,即 ,又
,又 ,所以
,所以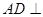 平面EGH,
平面EGH, ,又因为BF∥EH,所以AD
,又因为BF∥EH,所以AD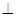 BF,在平行四边形ABCD中,BC∥AD,所以BC⊥BF;又GH⊥AD, GH∥ BD,所以BD ⊥AD,而BC∥AD,故BC⊥BD,所以BC⊥平面DFB,BC
BF,在平行四边形ABCD中,BC∥AD,所以BC⊥BF;又GH⊥AD, GH∥ BD,所以BD ⊥AD,而BC∥AD,故BC⊥BD,所以BC⊥平面DFB,BC 平面BCF,所以平面BCF⊥平面DFB,所以点D在平面BCF上的射影P点在BF上,所以∠FBD就是直线BD与平面BCF所成的角,在△BFD中, BF=HE=
平面BCF,所以平面BCF⊥平面DFB,所以点D在平面BCF上的射影P点在BF上,所以∠FBD就是直线BD与平面BCF所成的角,在△BFD中, BF=HE= ,又BC⊥平面DFB,所以,平面FBD⊥面ABCD,故F点在平面ABCD上的射影K在BD上,且FK=EG=
,又BC⊥平面DFB,所以,平面FBD⊥面ABCD,故F点在平面ABCD上的射影K在BD上,且FK=EG= ,所以
,所以 ,故求直线BD与平面BCF所成角是
,故求直线BD与平面BCF所成角是 。
。(第(Ⅱ)小题也可用向量解答,略)
点评:解决的关键是利用空间中的几何体的分割法来得到不规则几何体的体积的求解,对于角的求解可以运用几何法也可以运用向量法来得到。属于基础题。

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
 是三个不重合的平面,a,b是两条不重合的直线,有下列三个条件:①
是三个不重合的平面,a,b是两条不重合的直线,有下列三个条件:① ②
② ③
③ 如果命题
如果命题 且_______,则
且_______,则 为真命题,则可以在横线处填入的条件是( )
为真命题,则可以在横线处填入的条件是( )
 ,
, ,D为四面体OABC外一点.给出下列命题:①不存在点D,使四面体ABCD有三个面是直角三角形;②不存在点D,使四面体ABCD是正三棱锥;③存在点D,使CD与AB垂直并相等;④存在无数个点D,使点O在四面体ABCD的外接球面上.则其中正确命题的序号是( )
,D为四面体OABC外一点.给出下列命题:①不存在点D,使四面体ABCD有三个面是直角三角形;②不存在点D,使四面体ABCD是正三棱锥;③存在点D,使CD与AB垂直并相等;④存在无数个点D,使点O在四面体ABCD的外接球面上.则其中正确命题的序号是( ) ,A为PD的中点,如下左图。将
,A为PD的中点,如下左图。将 沿AB折到
沿AB折到 的位置,使
的位置,使 ,点E在SD上,且
,点E在SD上,且 ,如下图。
,如下图。 平面ABCD;
平面ABCD;
 中,对角线
中,对角线 于
于 ,
, ,
, 为
为 的重心,过点
的重心,过点 分别交
分别交 于
于 且
且 ,沿
,沿 将
将 折起,沿
折起,沿 折起,
折起, 正好重合于
正好重合于 .
. 
 平面
平面 ;
;  与平面
与平面 夹角的大小.
夹角的大小. 
 ;
; ,求AB的长.
,求AB的长.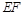 ⊥平面
⊥平面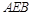 ,
,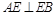 ,
,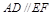 ,
,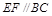 ,
,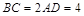 ,
,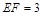 ,
,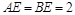 ,
,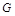 是
是 的中点.
的中点.
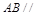 平面
平面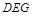 ;
;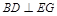 ;
;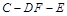 的余弦值.
的余弦值. 中,平面
中,平面 ∥平面
∥平面 ,
, ⊥平面
⊥平面 ,
, ,
,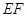 ∥
∥ .
. ,
,  .
.
 平面
平面 ;
; ∥平面
∥平面 ;
; 的余弦值.
的余弦值.