题目内容
如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB= ,AF=1,M是线段EF的中点.
,AF=1,M是线段EF的中点.

(Ⅰ)求证AM//平面BDE;
(Ⅱ)求二面角A-DF-B的大小;
(Ⅲ)试在线段AC上确定一点P,使得PF与BC所成的角是60°.
 ,AF=1,M是线段EF的中点.
,AF=1,M是线段EF的中点.
(Ⅰ)求证AM//平面BDE;
(Ⅱ)求二面角A-DF-B的大小;
(Ⅲ)试在线段AC上确定一点P,使得PF与BC所成的角是60°.
(1)对于线面平行的证明,主要是分析借助于中位线来得到AM∥OE
(2)60º(3)P是AC的中点
(2)60º(3)P是AC的中点
试题分析:解法一: (1)记AC与BD的交点为O,连接OE, ∵O、M分别是AC、EF的中点, ACEF是矩形,∴四边形AOEM是平行四边形,
∴AM∥OE.∵
 平面BDE,
平面BDE, 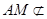 平面BDE,∴AM∥平面BDE.……4分
平面BDE,∴AM∥平面BDE.……4分(2)在平面AFD中过A作AS⊥DF于S,连结BS,∵AB⊥AF, AB⊥AD,
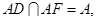 ∴AB⊥平面ADF,∴AS是BS在平面ADF上的射影,
∴AB⊥平面ADF,∴AS是BS在平面ADF上的射影,由三垂线定理得BS⊥DF.∴∠BSA是二面角A—DF—B的平面角.
在RtΔASB中,

∴
 ∴二面角A—DF—B的大小为60º.……8分
∴二面角A—DF—B的大小为60º.……8分(3)设CP=t(0≤t≤2),作PQ⊥AB于Q,则PQ∥AD,
∵PQ⊥AB,PQ⊥AF,
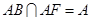 ,∴PQ⊥平面ABF,
,∴PQ⊥平面ABF, 平面ABF,∴PQ⊥QF.在RtΔPQF中,∠FPQ=60º,PF=2PQ.
平面ABF,∴PQ⊥QF.在RtΔPQF中,∠FPQ=60º,PF=2PQ.∵ΔPAQ为等腰直角三角形,∴
 又∵ΔPAF为直角三
又∵ΔPAF为直角三角形,∴
 ,∴
,∴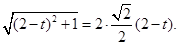 所以t=1或t=3(舍去),即点P是AC的中点.……12分
所以t=1或t=3(舍去),即点P是AC的中点.……12分解法二: (1)建立空间直角坐标系.
设
 ,连接NE, 则点N、E的坐标分别是(
,连接NE, 则点N、E的坐标分别是( 、(0,0,1),
、(0,0,1),∴
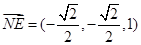 , 又点A、M的坐标分别是
, 又点A、M的坐标分别是 ,(
,(
∴
 =(
=( ∴
∴ 且NE与AM不共线,∴NE∥AM.又∵
且NE与AM不共线,∴NE∥AM.又∵ 平面BDE,
平面BDE, 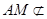 平面BDE,∴AM∥平面BDE.
平面BDE,∴AM∥平面BDE.(2)∵AF⊥AB,AB⊥AD,AF
 ∴AB⊥平面ADF.
∴AB⊥平面ADF.∴

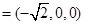 为平面DAF的法向量.
为平面DAF的法向量.∵
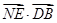 =(
=( ·
·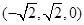 =0,
=0,∴
 =(
=( ·
· =0得
=0得 ,
, ,∴NE为平面BDF的法向量.
,∴NE为平面BDF的法向量.∴cos<
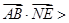 =
=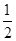 ∴AB与NE的夹角是60º.即所求二面角A—DF—B的大小是60º.
∴AB与NE的夹角是60º.即所求二面角A—DF—B的大小是60º.(3)设P(t,t,0)(0≤t≤
 )得
)得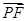
 ∴
∴ =(0,
=(0, , 0)
, 0)又∵PF和BC所成的角是60º.∴

解得
 或
或 (舍去),即点P是AC的中点.
(舍去),即点P是AC的中点.点评:解决的关键是根据线面平行的判定定理,以及空间的法向量来求解二面角的平面角的大小,属于中档题。

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
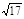 ,则这个二面角的大小为( )
,则这个二面角的大小为( )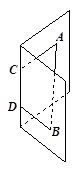





 ={直线},
={直线}, ={平面},
={平面}, .若
.若 ,给出下列四个命题:
,给出下列四个命题: ②
② ③
③ ④
④ 其中所有正确命题的序号是 .
其中所有正确命题的序号是 . 是三个不重合的平面,a,b是两条不重合的直线,有下列三个条件:①
是三个不重合的平面,a,b是两条不重合的直线,有下列三个条件:① ②
② ③
③ 如果命题
如果命题 且_______,则
且_______,则 为真命题,则可以在横线处填入的条件是( )
为真命题,则可以在横线处填入的条件是( ) 的底面
的底面 为一直角梯形,其中
为一直角梯形,其中 ,
,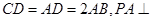 底面
底面 是
是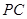 的中点.
的中点.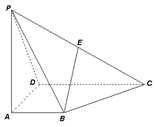
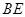 //平面
//平面 ;
; 平面
平面 ,求平面
,求平面 与平面
与平面 夹角的余弦值.
夹角的余弦值.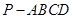 中,
中,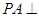 底面
底面 ,
,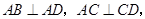
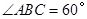 ,
,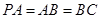 ,
,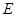 是
是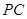 的中点.
的中点.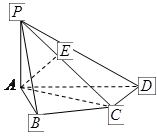
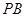 和平面
和平面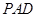 所成的角的大小;
所成的角的大小;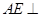 平面
平面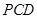 ;
;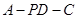 的正弦值.
的正弦值.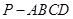 的底面是正方形,
的底面是正方形,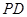 ⊥底面
⊥底面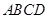 ,点
,点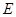 在棱
在棱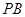 上.
上.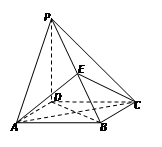
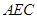 ⊥平面
⊥平面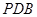 ;
;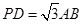 且
且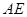 与平面
与平面

 ;
; ,求AB的长.
,求AB的长.