题目内容
7.已知函数f(x)=lnx+$\frac{1-x}{ax}$,其中a≠0(1)当a=1时,求曲线y=f(x)在点(1,f(1))处的切线方程
(2)若函数f(x)是[1,+∞)上为增函数,求非零实数a的取值范围.
分析 (1)求导数f′(x),可得切线斜率,切点为(1,0),由点斜式可求切线方程;
(2)由f(x)在(0,+∞)上为单调增函数,知f'(x)≥0在(0,+∞)上恒成立,分离出参数a后,转化为求函数的最值.
解答 解:(1)当a=1时,f′(x)=$\frac{1}{x}$-$\frac{1}{{x}^{2}}$,
∴f′(1)=0,f(1)=0,
∴曲线y=f(x)在点(1,f(1))处的切线方程是y=0;
(2)f′(x)=$\frac{1}{x}$-$\frac{1}{a{x}^{2}}$,
∵函数f(x)是[1,+∞)上为增函数,
∴$\frac{1}{x}$-$\frac{1}{a{x}^{2}}$≥0在[1,+∞)上恒成立,
∴a≥$\frac{1}{x}$在[1,+∞)上恒成立,
∴a≥1.
点评 该题考查导数的几何意义、利用导数研究函数的单调性,考查函数恒成立,考查转化思想.

练习册系列答案
 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
4. “累积净化量(CCM)”是空气净化器质量的一个重要衡量指标,它是指空气净化器从开始使用到净化效率为50%时对颗粒物的累积净化量,以克表示.根据GB/T18801-2015《空气净化器》国家标准,对空气净化器的累积净化量(CCM)有如下等级划分:
“累积净化量(CCM)”是空气净化器质量的一个重要衡量指标,它是指空气净化器从开始使用到净化效率为50%时对颗粒物的累积净化量,以克表示.根据GB/T18801-2015《空气净化器》国家标准,对空气净化器的累积净化量(CCM)有如下等级划分:
为了了解一批空气净化器(共2000台)的质量,随机抽取n台机器作为样本进行估计,已知这n台机器的
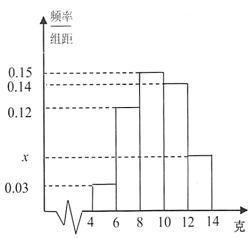
累积净化量都分布在区间(4,14]中,按照(4,6],(6,8],(8,10],(10,12],(12,14],均匀分组,其中累积净化量在(4,6]的所有数据有:4.5,4.6,5.2,5.7和5.9,并绘制了如下频率分布直方图.
(Ⅰ)求n的值及频率分布直方图中的x值;
(Ⅱ)以样本估计总体,试估计这批空气净化器(共2000台)中等级为P2的空气净化器有多少台?
(Ⅲ)从累积净化量在(4,6]的样本中随机抽取2台,求恰好有1台等级为P2的概率.
 “累积净化量(CCM)”是空气净化器质量的一个重要衡量指标,它是指空气净化器从开始使用到净化效率为50%时对颗粒物的累积净化量,以克表示.根据GB/T18801-2015《空气净化器》国家标准,对空气净化器的累积净化量(CCM)有如下等级划分:
“累积净化量(CCM)”是空气净化器质量的一个重要衡量指标,它是指空气净化器从开始使用到净化效率为50%时对颗粒物的累积净化量,以克表示.根据GB/T18801-2015《空气净化器》国家标准,对空气净化器的累积净化量(CCM)有如下等级划分:| 累积净化量(克) | (3,5] | (5,8] | (8,12] | 12以上 |
| 等级 | P1 | P2 | P3 | P4 |
累积净化量都分布在区间(4,14]中,按照(4,6],(6,8],(8,10],(10,12],(12,14],均匀分组,其中累积净化量在(4,6]的所有数据有:4.5,4.6,5.2,5.7和5.9,并绘制了如下频率分布直方图.
(Ⅰ)求n的值及频率分布直方图中的x值;
(Ⅱ)以样本估计总体,试估计这批空气净化器(共2000台)中等级为P2的空气净化器有多少台?
(Ⅲ)从累积净化量在(4,6]的样本中随机抽取2台,求恰好有1台等级为P2的概率.
12.已知函数f(x)是奇函数,当x<0时,f(x)=xln(-x)+x+2,则曲线y=f(x)在x=1处的切线方程为( )
| A. | y=2x+3 | B. | y=2x-3 | C. | y=-2x+3 | D. | y=-2x-3 |
16.定义在R上的奇函数f(x)关于点(2,1)对称,则f(6)=( )
| A. | 9 | B. | 7 | C. | 5 | D. | 3 |
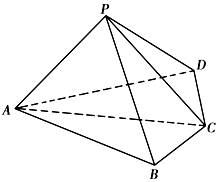 如图,四棱锥P-ABCD中,平面PAC⊥平面ABCD,AC=2BC=2CD=4,∠ACB=∠ACD=60°.
如图,四棱锥P-ABCD中,平面PAC⊥平面ABCD,AC=2BC=2CD=4,∠ACB=∠ACD=60°.