题目内容
12.已知函数f(x)是奇函数,当x<0时,f(x)=xln(-x)+x+2,则曲线y=f(x)在x=1处的切线方程为( )| A. | y=2x+3 | B. | y=2x-3 | C. | y=-2x+3 | D. | y=-2x-3 |
分析 利用奇函数的性质,求出x>0时,函数的解析式,求导函数,确定切线的斜率,求得切点坐标,进而可求切线方程.
解答 解:设x>0,则-x<0,f(-x)=-xlnx-x+2,
∵函数f(x)是奇函数,
∴f(x)=-f(-x)=xlnx+x-2,
∴f′(x)=lnx+2,
x=1,f′(1)=2,f(1)=-1,
∴曲线y=f(x)在x=1处的切线方程为y=2x-3,
故选B.
点评 本题考查奇函数的性质,考查导数知识的运用,考查导数的几何意义,求出切线的斜率是关键,属于中档题.

练习册系列答案
相关题目
1.某几何体的三视图如图所示,则该几何体的体积为( )
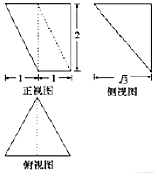

| A. | $\frac{11}{6}$$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | $\frac{5\sqrt{3}}{3}$ | D. | $\frac{4\sqrt{3}}{3}$ |
2.已知i是虚数单位,则(1+i)2的共轭复数是( )
| A. | -2i | B. | -2+i | C. | 2i | D. | 1+2i |
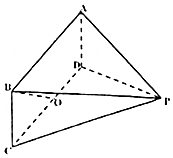 如图,已知四边形ABCD是矩形,AB=2BC=2,三角形PCD是正三角形,且平面ABCD⊥平面PCD.
如图,已知四边形ABCD是矩形,AB=2BC=2,三角形PCD是正三角形,且平面ABCD⊥平面PCD.