题目内容
4. “累积净化量(CCM)”是空气净化器质量的一个重要衡量指标,它是指空气净化器从开始使用到净化效率为50%时对颗粒物的累积净化量,以克表示.根据GB/T18801-2015《空气净化器》国家标准,对空气净化器的累积净化量(CCM)有如下等级划分:
“累积净化量(CCM)”是空气净化器质量的一个重要衡量指标,它是指空气净化器从开始使用到净化效率为50%时对颗粒物的累积净化量,以克表示.根据GB/T18801-2015《空气净化器》国家标准,对空气净化器的累积净化量(CCM)有如下等级划分:| 累积净化量(克) | (3,5] | (5,8] | (8,12] | 12以上 |
| 等级 | P1 | P2 | P3 | P4 |
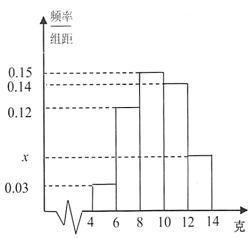
累积净化量都分布在区间(4,14]中,按照(4,6],(6,8],(8,10],(10,12],(12,14],均匀分组,其中累积净化量在(4,6]的所有数据有:4.5,4.6,5.2,5.7和5.9,并绘制了如下频率分布直方图.
(Ⅰ)求n的值及频率分布直方图中的x值;
(Ⅱ)以样本估计总体,试估计这批空气净化器(共2000台)中等级为P2的空气净化器有多少台?
(Ⅲ)从累积净化量在(4,6]的样本中随机抽取2台,求恰好有1台等级为P2的概率.
分析 (Ⅰ)先求出在(4,6]之间的数据一共有6个,再由频布直方图得:落在(4,6]之间的频率为0.03×2=0.06,由此能求出n的值及频率分布直方图中的x值.
(Ⅱ)由频率分布直方图可知:落在(6,8]之间共24台,在(5,6]之间共4台,从而落在(5,8]之间共28台,由此能估计这批空气净化器(共2000台)中等级为P2的空气净化器有多少台.
(Ⅲ)设“恰好有1台等级为P2”为事件B,依题意落在(4,6]之间共6台,属于国标P2级的有4台,则从(4,6]中随机抽取2台,基本事件总数n=${C}_{6}^{2}=15$,事件B包含的基本事件个数m=${C}_{4}^{1}{C}_{2}^{1}$=8,由此能求出恰好有1台等级为P2的概率.
解答 解:(Ⅰ)∵在(4,6]之间的数据一共有6个,
再由频布直方图得:落在(4,6]之间的频率为0.03×2=0.06,
∴n=$\frac{6}{0.06}$=100,
由频率分布直方图的性质得:
(0.03+x+0.12+0.14+0.15)×2=1,
解得x=0.06.
(Ⅱ)由频率分布直方图可知:落在(6,8]之间共:0.12×2×100=24台,
又∵在(5,6]之间共4台,
∴落在(5,8]之间共28台,
∴估计这批空气净化器(共2000台)中等级为P2的空气净化器有560台.
(Ⅲ)设“恰好有1台等级为P2”为事件B,
依题意落在(4,6]之间共6台,属于国标P2级的有4台,
则从(4,6]中随机抽取2台,基本事件总数n=${C}_{6}^{2}=15$,
事件B包含的基本事件个数m=${C}_{4}^{1}{C}_{2}^{1}$=8,
∴恰好有1台等级为P2的概率P(B)=$\frac{m}{n}=\frac{8}{15}$.
点评 本题考查频率分布直方图的求法,考查概率的求法,是基础题,解题时要认真审题,注意等可能事件概率计算公式的合理运用.

| A. | $\sqrt{3}$+1 | B. | $\sqrt{6}$+$\sqrt{2}$ | C. | $\sqrt{6}$+2 | D. | $\sqrt{3}+$$\sqrt{2}$ |
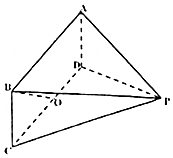 如图,已知四边形ABCD是矩形,AB=2BC=2,三角形PCD是正三角形,且平面ABCD⊥平面PCD.
如图,已知四边形ABCD是矩形,AB=2BC=2,三角形PCD是正三角形,且平面ABCD⊥平面PCD.