题目内容
已知
,则z=2x-y的最小值是 .
|
考点:简单线性规划
专题:计算题
分析:作出题中不等式组表示的平面区域,得如图的△ABC及其内部,再将目标函数z=2x-y对应的直线进行平移并观察z的变化,即可得到z=2x-y的最小值.
解答:
解: 作出不等式组
作出不等式组
表示的平面区域,得到如图所示的阴影表示的区域,其中A(-2,0),B(0,-2),
将直线l:z=2x-y平行平移,
由于z表示直线z=2x-y的截距的相反数,
当l经过点B时,目标函数z达到最大值;l经过点A时,目标函数z达到最小值
∴z最大值=2;z最小值=2×(-2)-0=-4
即z=2x-y的最小值是-4.
故答案为:-4
 作出不等式组
作出不等式组
|
将直线l:z=2x-y平行平移,
由于z表示直线z=2x-y的截距的相反数,
当l经过点B时,目标函数z达到最大值;l经过点A时,目标函数z达到最小值
∴z最大值=2;z最小值=2×(-2)-0=-4
即z=2x-y的最小值是-4.
故答案为:-4
点评:本题考查了简单的线性规划,解答的关键是正确作出可行域,属于中档题.

练习册系列答案
相关题目
 执行如图所示的程序框图,任意输入一次x(0≤x≤1)与y(0≤y≤1),则能输出数对(x,y)的概率为( )
执行如图所示的程序框图,任意输入一次x(0≤x≤1)与y(0≤y≤1),则能输出数对(x,y)的概率为( )A、
| ||
B、
| ||
C、
| ||
D、
|
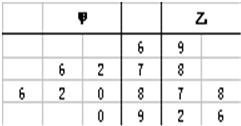 如图是甲、乙两名同学的六次测试成绩的茎叶图,下列说法正确的是( )
如图是甲、乙两名同学的六次测试成绩的茎叶图,下列说法正确的是( )①甲同学成绩的中位数大于乙同学成绩的中位数;
②甲同学的平均分比乙同学平均分高;
③甲同学成绩的平均分比乙同学平均分低;
④甲同学成绩的方差小于乙同学成绩的方差.
| A、①③ | B、①②④ | C、③④ | D、③ |
设P是圆(x-3)2+(y+1)2=4上的动点,Q是直线x=-3上的动点,则|PQ|的最小值为( )
| A、6 | B、4 | C、3 | D、2 |
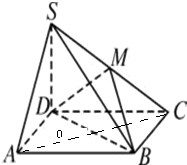 如图,底面ABCD是正方形,SD=AD,SD⊥底面ABCD,M为SC中点.求直线DM与SB所成的角的余弦值.
如图,底面ABCD是正方形,SD=AD,SD⊥底面ABCD,M为SC中点.求直线DM与SB所成的角的余弦值.