题目内容
已知数列{an}满足an=n(n+1)(n+2)(n+3),求数列{an}的前n项和Sn.
考点:数列的求和
专题:点列、递归数列与数学归纳法
分析:利用n(n+1)(n+2)(n+3)=4!
及组合数的性质
+
=
即可求得数列{an}的前n项和Sn.
| C | 4 n+3 |
| C | m-1 n |
| C | m n |
| C | m n+1 |
解答:
解:∵n(n+1)(n+2)(n+3)=4!
,
∴Sn=4!(
+
+
+…+
)
=4!(
+
+
+…+
)
=4!(
+
+
+…+
)
=4!(
+
+…+
)
=4!(
+
+…+
)
=4!
,
=
(n+4)(n+3)(n+2)(n+1)n.
| C | 4 n+3 |
∴Sn=4!(
| C | 4 1+3 |
| C | 4 2+3 |
| C | 4 3+3 |
| C | 4 n+3 |
=4!(
| C | 4 4 |
| C | 4 5 |
| C | 4 6 |
| C | 4 n+3 |
=4!(
| C | 5 5 |
| C | 4 5 |
| C | 4 6 |
| C | 4 n+3 |
=4!(
| C | 5 6 |
| C | 4 6 |
| C | 4 n+3 |
=4!(
| C | 5 7 |
| C | 4 7 |
| C | 4 n+3 |
=4!
| C | 5 n+4 |
=
| 1 |
| 5 |
点评:本题考查数列的求和,分析出n(n+1)(n+2)(n+3)=4!
是关键,考查组合数的性质,属于难题.
| C | 4 n+3 |

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
已知集合M={x|x≥-1},N={x|2-x2≥0},则M∪N=( )
A、[-
| ||
B、[-1,
| ||
| C、[-1,+∞) | ||
D、(-∞,-
|
已知抛物线y2=6x的焦点F,点P在抛物线上,M(-1,0)若
•
=5,则以点M为圆心,过点P的圆的方程为( )
| PM |
| PF |
| A、x2+y2+2x-7=0 |
| B、x2+y2+2x-9=0 |
| C、x2+y2+2x-11=0 |
| D、x2+y2+2x-13=0 |
sin2013°的值属于区间( )
A、(-
| ||
B、(-1,-
| ||
C、(
| ||
D、(0,
|
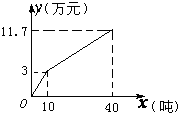 春节前夕,南方地区遭遇罕见的低温雨雪冰冻天气,赣南脐橙受灾滞销.为了减少果农的损失,政府部门出台了相关补贴政策:采取每千克补贴0.2元的办法补偿果农.如图是“绿荫”果园受灾期间政府补助前、后脐橙销售总收入y(万元)与销售量x(吨)的关系图.请结合图象回答以下问题:
春节前夕,南方地区遭遇罕见的低温雨雪冰冻天气,赣南脐橙受灾滞销.为了减少果农的损失,政府部门出台了相关补贴政策:采取每千克补贴0.2元的办法补偿果农.如图是“绿荫”果园受灾期间政府补助前、后脐橙销售总收入y(万元)与销售量x(吨)的关系图.请结合图象回答以下问题: