题目内容
关于三角函数f(x)=sin(x+
π)的图象,下列说法正确的是( )
| 3 |
| 2 |
| A、f(x)是奇函数 | ||
B、f(x)的图象关于直线x=
| ||
| C、f(x)的周期为π | ||
D、f(x)的图象关于点(
|
考点:正弦函数的图象
专题:三角函数的图像与性质
分析:由条件利用诱导公式、余弦函数的图象和性质得出结论.
解答:
解:由于三角函数f(x)=sin(x+
π)=-cosx,显然是偶函数,故排除A;
它的周期为2π,故排除C;
当x=
时,函数f(x)=0,故f(x)的图象关于点(
,0)对称,故排除B,且D正确,
故选:D.
| 3 |
| 2 |
它的周期为2π,故排除C;
当x=
| π |
| 2 |
| π |
| 2 |
故选:D.
点评:本题主要考查诱导公式、余弦函数的图象和性质,属于基础题.

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
在△ABC中,角A,B,C所对的边分别为a,b,c,若sin2B+sin2C-sin2A+sinBsinC=0,则tanA的值是( )
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
△ABC中,若a=1,c=4,B=120°,则△ABC的面积为( )
| A、1 | ||
B、
| ||
| C、2 | ||
D、2
|
已知等差数列{an}的前n项和为Sn,若a6=16-a4,则S9等于( )
| A、32 | B、18 | C、72 | D、64 |
某单位分别有老、中、青职工500,1000,800人.为了解职工身体状况,现按5:10:8的比例从中抽取230人进行检查,则这种抽样方法是( )
| A、抽签法 | B、随机数表法 |
| C、分层抽样 | D、系统抽样 |
一个正方体内接于一个球,过球心作一个截面,则截面不可能的图形为( )
A、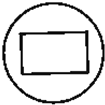 |
B、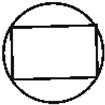 |
C、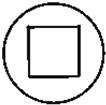 |
D、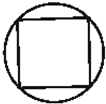 |