题目内容
若存在实常数k和b,使得函数F(x)和G(x)对其公共定义域上的任意实数x都满足:F(x)≥kx+b和G(x)≤kx+b恒成立,则称此直线y=kx+b为F(x)和G(x)的“隔离直线”.已知函数f(x)=x2(x∈R),g(x)=
(x<0),h(x)=2elnx.有下列命题:
①F(x)=f(x)-g(x)在x∈(-
,0)内单调递增;
②f(x)和g(x)之间存在“隔离直线”,且b的最小值为-4;
③f(x)和g(x)之间存在“隔离直线”,且k的取值范围是(-4,0];
④f(x)和h(x)之间存在唯一的“隔离直线”y=2
x-e.
其中真命题的个数有( )
| 1 |
| x |
①F(x)=f(x)-g(x)在x∈(-
| 1 | |||
|
②f(x)和g(x)之间存在“隔离直线”,且b的最小值为-4;
③f(x)和g(x)之间存在“隔离直线”,且k的取值范围是(-4,0];
④f(x)和h(x)之间存在唯一的“隔离直线”y=2
| e |
其中真命题的个数有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
考点:命题的真假判断与应用
专题:新定义,函数的性质及应用,导数的综合应用
分析:①求出F(x)=f(x)-g(x)的导数,检验在x∈(-
,0)内的导数符号,即可判断;
②、③设f(x)、g(x)的隔离直线为y=kx+b,x2≥kx+b对一切实数x成立,即有△1≤0,又
≤kx+b对一切x<0成立,△2≤0,k≤0,b≤0,根据不等式的性质,求出k,b的范围,即可判断②③;
④存在f(x)和g(x)的隔离直线,那么该直线过这个公共点,设隔离直线的斜率为k.则隔离直线,构造函数,求出函数函数的导数,根据导数求出函数的最值.
| 1 | |||
|
②、③设f(x)、g(x)的隔离直线为y=kx+b,x2≥kx+b对一切实数x成立,即有△1≤0,又
| 1 |
| x |
④存在f(x)和g(x)的隔离直线,那么该直线过这个公共点,设隔离直线的斜率为k.则隔离直线,构造函数,求出函数函数的导数,根据导数求出函数的最值.
解答:
解:①∵F(x)=f(x)-g(x)=x2-
,∴x∈(-
,0),F′(x)=2x+
>0,
∴F(x)=f(x)-g(x)在x∈(-
,0)内单调递增,故①对;
②、③设f(x)、g(x)的隔离直线为y=kx+b,则x2≥kx+b对一切实数x成立,即有△1≤0,k2+4b≤0,
又
≤kx+b对一切x<0成立,则kx2+bx-1≤0,即△2≤0,b2+4k≤0,k≤0,b≤0,
即有k2≤-4b且b2≤-4k,k4≤16b2≤-64k⇒-4≤k≤0,同理⇒-4≤b≤0,故②对,③错;
④函数f(x)和h(x)的图象在x=
处有公共点,因此存在f(x)和g(x)的隔离直线,
那么该直线过这个公共点,设隔离直线的斜率为k.则隔离直线方程为y-e=k(x-
),即y=kx-k
+e,
由f(x)≥kx-k
+e(x∈R),可得x2-kx+k
-e≥0当x∈R恒成立,
则△≤0,只有k=2
,此时直线方程为:y=2
x-e,
下面证明h(x)≤2
x-e,令G(x)=2
x-e-h(x)=2
x-e-2elnx,
G′(x)=
,
当x=
时,G′(x)=0,当0<x<
时G′(x)<0,当x>
时G′(x)>0,
则当x=
时,G(x)取到极小值,极小值是0,也是最小值.
所以G(x)=2
x-e-g(x)≥0,则g(x)≤2
x-e当x>0时恒成立.
∴函数f(x)和g(x)存在唯一的隔离直线y=2
x-e,故④正确.
故选:C.
| 1 |
| x |
| 1 | |||
|
| 1 |
| x2 |
∴F(x)=f(x)-g(x)在x∈(-
| 1 | |||
|
②、③设f(x)、g(x)的隔离直线为y=kx+b,则x2≥kx+b对一切实数x成立,即有△1≤0,k2+4b≤0,
又
| 1 |
| x |
即有k2≤-4b且b2≤-4k,k4≤16b2≤-64k⇒-4≤k≤0,同理⇒-4≤b≤0,故②对,③错;
④函数f(x)和h(x)的图象在x=
| e |
那么该直线过这个公共点,设隔离直线的斜率为k.则隔离直线方程为y-e=k(x-
| e |
| e |
由f(x)≥kx-k
| e |
| e |
则△≤0,只有k=2
| e |
| e |
下面证明h(x)≤2
| e |
| e |
| e |
G′(x)=
2
| ||||
| x |
当x=
| e |
| e |
| e |
则当x=
| e |
所以G(x)=2
| e |
| e |
∴函数f(x)和g(x)存在唯一的隔离直线y=2
| e |
故选:C.
点评:本题以函数为载体,考查新定义,关键是对新定义的理解,考查函数的求导,利用导数求最值,属于难题.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
某单位分别有老、中、青职工500,1000,800人.为了解职工身体状况,现按5:10:8的比例从中抽取230人进行检查,则这种抽样方法是( )
| A、抽签法 | B、随机数表法 |
| C、分层抽样 | D、系统抽样 |
如图所示程序运行结果是( )


| A、-8 | B、4 | C、-20 | D、20 |
下列说法错误的是( )
A、“sinθ=
| ||
| B、命题“若a=0,则ab=0”的否命题是:“若a≠0,则ab≠0” | ||
| C、若命题p:?x∈R,x2-x+1<0,则¬p:?x∈R,x2-x+1≥0 | ||
| D、函数y=log2(x2-2x)的单调增区间是[1,+∞) |
已知a,b∈R+,且满足a,b,a+b成等差数列,a,b,ab2成等比数列,则关于x的不等式ax2-bx+1≤0的解集为( )
| A、{1} | B、[-1,2] |
| C、R | D、∅ |
一个正方体内接于一个球,过球心作一个截面,则截面不可能的图形为( )
A、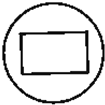 |
B、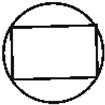 |
C、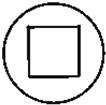 |
D、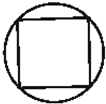 |