题目内容
已知关于x的一元二次方程x2+(m-3)x-
(n2-4n)=0.
(1)m和n分别是抛掷两枚骰子得到的点数,求上述方程有根的概率.
(2)若m,n∈R且0≤m≤6,0≤n≤6,求上述方程有根的概率.
| 1 |
| 4 |
(1)m和n分别是抛掷两枚骰子得到的点数,求上述方程有根的概率.
(2)若m,n∈R且0≤m≤6,0≤n≤6,求上述方程有根的概率.
考点:列举法计算基本事件数及事件发生的概率,几何概型
专题:概率与统计
分析:(1)本题是一个等可能事件的概率,试验发生包含的事件数是6×6=36种结果,方程有实根要满足判别式不小于0,即满足(m-3)2+(n-2)2≥4,根据点和圆的位置关系,即可求出满足条件的基本事件,根据概率公式计算即可
(2)根据几何概型的概率求法,如图所示,即可求出
(2)根据几何概型的概率求法,如图所示,即可求出
解答:
 解:由题意知本题是一个等可能事件的概率,试验发生包含的事件数是6×6=36种结果,
解:由题意知本题是一个等可能事件的概率,试验发生包含的事件数是6×6=36种结果,
方程x2+(m-3)x-
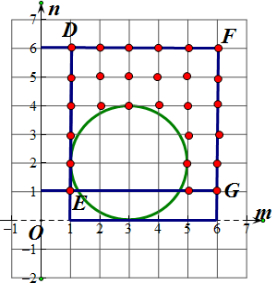
(n2-4n)=0.有实根要满足(m-3)2+(n2-4n)≥0,即(m-3)2+(n-2)2≥4,如图所示
表示在以(3,2)位圆心以2位半径的圆的外部或圆上,共有27种结果
故方程有根的概率P=
=
,
(2)试验的全部结果所构成的区域为Ω={(m,n)|0≤m≤6,0≤n≤6}.
构成事件A的区域为{(a,b)|((m-3)2+(n-2)2≥4}.
如图四边形DEGF的面积为7×7=49,
而圆的面积为4π,
则事件A的区域的面积为49-4π,
∴所以所求的概率P=
=1-
 解:由题意知本题是一个等可能事件的概率,试验发生包含的事件数是6×6=36种结果,
解:由题意知本题是一个等可能事件的概率,试验发生包含的事件数是6×6=36种结果,方程x2+(m-3)x-
| 1 |
| 4 |
表示在以(3,2)位圆心以2位半径的圆的外部或圆上,共有27种结果
故方程有根的概率P=
| 27 |
| 36 |
| 3 |
| 4 |
(2)试验的全部结果所构成的区域为Ω={(m,n)|0≤m≤6,0≤n≤6}.
构成事件A的区域为{(a,b)|((m-3)2+(n-2)2≥4}.
如图四边形DEGF的面积为7×7=49,
而圆的面积为4π,
则事件A的区域的面积为49-4π,
∴所以所求的概率P=
| 49-4π |
| 49 |
| 4π |
| 49 |
点评:本题考查了古典概型和几何概型的概率的求法,关键是画出图象,属于中档题

练习册系列答案
相关题目
i是虚数单位,复数
在复平面上的对应点所在直线方程是( )
| 2-i |
| 1+i |
| A、x+y-2=0 |
| B、x-y+2=0 |
| C、x+y+1=0 |
| D、x-y-1=0 |
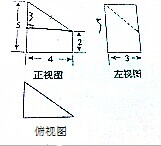 某几何体的三视图如图所示,则该几何体的表面积为( )
某几何体的三视图如图所示,则该几何体的表面积为( )| A、54 | B、60 | C、66 | D、72 |
使
=
成立的α范围( )
|
| cosα-1 |
| sinα |
| A、{x|2kπ-π<α<2kπ,k∈Z} | ||
| B、{x|2kπ-π≤α≤2kπ,k∈Z} | ||
C、{x|2kπ+π<α<2kπ+
| ||
| D、只能是第三或第四象限的角 |