题目内容
偶函数f（x）对任意实数x满足f（x+2）=f（x），且当2≤x≤3时，f（x）=x，则当-2≤x≤0时，f（x）的表达式为 ．
考点：抽象函数及其应用,函数解析式的求解及常用方法
专题：函数的性质及应用
分析：先判断出函数为周期函数，再根据偶函数的性质，继而求出函数的解析式．
解答：
解：∵f（x+2）=f（x），
∴函数f（x）以2为最小正周期的周期函数，（图象如图所示）
当-2≤x≤-1时，
∴2≤x+4≤3，
∴f（x+4）=x+4=f（x），
∴f（x）=x+4，
∵函数f（x）为偶函数，
同理可求，
当-1≤x≤0时，
∴f（x）=-x+2
∴f（x）=
故答案为：f（x）=
解：∵f（x+2）=f（x），∴函数f（x）以2为最小正周期的周期函数，（图象如图所示）
当-2≤x≤-1时，
∴2≤x+4≤3，
∴f（x+4）=x+4=f（x），
∴f（x）=x+4，
∵函数f（x）为偶函数，
同理可求，
当-1≤x≤0时，
∴f（x）=-x+2
∴f（x）=
|
故答案为：f（x）=
|
点评：本题考查的知识点是函数奇偶性与单调性的综合应用，函数的周期性，属于中档题．
练习册系列答案
期末1卷素质教育评估卷系列答案
相关题目
如图，从甲、乙两种玉米苗中各抽6株，分别测得它们的株高如下（单位：cm）：根据以下数据估计（ ）
| A、甲种玉米比乙种玉米不仅长得高而且长得整齐 |
| B、乙种玉米比甲种玉米不仅长得高而且长得整齐 |
| C、甲种玉米比乙种玉米长得高但长势没有乙整齐 |
| D、乙种玉米比甲种玉米长得高但长势没有甲整齐 |
以下程序的功能是（ ）
| A、计算3×10的值 |
| B、计算355的值 |
| C、计算310的值 |
| D、计算1×2×3×…×10的值 |
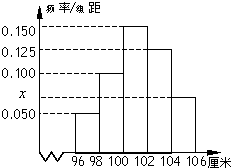某幼儿园根据部分同年龄段女童的身高数据绘制了频率分布直方图，其中身高的变化范围是[96，106]（单位：厘米），样本数据分组为[96，98），[98，100），[100，102），[102，104），[104，106]．