题目内容
9.在六条棱长分别为2、3、3、4、5、5的所有四面体中,最大的体积是( )| A. | $\frac{{8\sqrt{2}}}{3}$ | B. | $\frac{{5\sqrt{11}}}{6}$ | C. | $\frac{{\sqrt{462}}}{4}$ | D. | $2\sqrt{6}$ |
分析 由题意画出适合题意的四面体,求出每种情况的体积比较得答案.
解答 解:由题意可知,由棱长2、3、3、4、5、5构成的四面体有如下三种情况: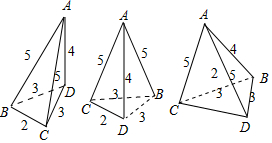
左图中,由于32+42=52,即图中AD⊥平面BCD,
∴V1=$\frac{1}{3}×\frac{1}{2}×2\sqrt{{3}^{2}-{1}^{2}}×4=\frac{8\sqrt{2}}{3}$;
中间图,由于此情况的底面与上相同,但AC不与底垂直,故高<4,于是得 V2<V1;
右图中,高<2,底面积$\frac{1}{2}×5×\sqrt{{3}^{2}-(\frac{5}{2})^{2}}=\frac{5}{4}\sqrt{11}$.
∴V3<$\frac{1}{3}×\frac{5}{4}\sqrt{11}=\frac{5}{6}\sqrt{11}$<$\frac{8\sqrt{2}}{3}$.
∴最大体积为$\frac{8\sqrt{2}}{3}$.
故选:A.
点评 本题考查了棱锥的体积和表面积,考查了学生的空间想象能力,考查了分类讨论的数学思想方法,此题是中档题.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
19.设Sn为等差数列{an}的前n项和,S8=4a3,a7=-2,则a9=( )
| A. | -6 | B. | -4 | C. | -2 | D. | 2 |
20.设变量x,y满足约束条件$\left\{\begin{array}{l}x+y≥2\\ 2x+y≥2\\ x-y≤2\end{array}\right.$目标函数z=x-2y的最大值是( )
| A. | -4 | B. | 2 | C. | $\frac{8}{3}$ | D. | $\frac{16}{3}$ |
17.已知幂函数y=f(x)的图象过点$(2\;,\;\;\sqrt{2})$,则$f({\frac{1}{3}})$的值为( )
| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $\frac{1}{3}$ | C. | 3 | D. | 1 |
4.已知双曲线mx2+y2=1(m∈R)与椭圆${x^2}+\frac{y^2}{5}=1$有相同的焦点,则该双曲线的渐近线方程为( )
| A. | $y=±\sqrt{3}x$ | B. | $y=±\frac{{\sqrt{3}}}{3}x$ | C. | $y=±\frac{1}{3}x$ | D. | y=±3x |
14.命题“?x∈R,ex-x-1<0”的否定是( )
| A. | ?x∈R,ex-x-1≥0 | B. | ?x∈R,ex-x-1>0 | C. | ?x∈R,ex-x-1>0 | D. | ?x∈R,ex-x-1≥0 |
1.定义2×2矩阵$[\begin{array}{l}{{a}_{1}}&{{a}_{2}}\\{{a}_{3}}&{{a}_{4}}\end{array}]$=a1a4-a2a3,若f(x)=$[\begin{array}{l}{cosx-sinx}&{\sqrt{3}}\\{cos(\frac{π}{2}+2x)}&{cosx+sinx}\end{array}]$,则f(x)( )
| A. | 图象关于(π,0)中心对称 | B. | 图象关于直线$x=\frac{π}{2}$对称 | ||
| C. | 在区间$[-\frac{π}{6},0]$上单调递增 | D. | 周期为π的奇函数 |
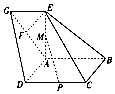 如图,四边形ABCD是正方形,且平面ABCD⊥平面ABEG,F是AG上一点,且△ABE与△AEF都是等腰直角三角形,AB=AE,AF=EF.
如图,四边形ABCD是正方形,且平面ABCD⊥平面ABEG,F是AG上一点,且△ABE与△AEF都是等腰直角三角形,AB=AE,AF=EF.