题目内容
18.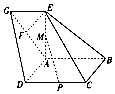 如图,四边形ABCD是正方形,且平面ABCD⊥平面ABEG,F是AG上一点,且△ABE与△AEF都是等腰直角三角形,AB=AE,AF=EF.
如图,四边形ABCD是正方形,且平面ABCD⊥平面ABEG,F是AG上一点,且△ABE与△AEF都是等腰直角三角形,AB=AE,AF=EF.(1)求证:EF⊥平面BCE;
(2)设线段CD,AE的中点分别为P,M,求三棱锥M-BDP和三棱锥F-BCE的体积比.
分析 (1)推导出BC⊥平面ABEG,从而EF⊥BC,再求出EF⊥BE,由此能证明EF⊥平面BCE.
(2)设正方形ABCD的边长为a,连结MB,MD,BD,BP,VM-BDP=$\frac{1}{3}{S}_{△BDP}×MA$;同理,连接FB,FC,则VF-BCE=$\frac{1}{3}{S}_{△BCE}×EF$,由此能求出三棱锥M-BDP和三棱锥F-BCE的体积比.
解答 证明:(1)∵平面ABCD⊥平面ABEG,平面ABCD∩平面ABEG=AB,
ABCD为正方形,
∴BC⊥平面ABEG,∵EF?平面ABEG,∴EF⊥BC,
∵$∠AEF+∠AEB=\frac{π}{2}$,∴EF⊥BE,
又BE?平面BCE,BC?平面BCE,BC∩BE=B,
∴EF⊥平面BCE.
解:(2)设正方形ABCD的边长为a,连结MB,MD,BD,BP,
则VM-BDP=$\frac{1}{3}{S}_{△BDP}×MA$=$\frac{1}{3}×\frac{{a}^{2}}{4}×\frac{a}{2}=\frac{{a}^{3}}{24}$,
同理,连接FB,FC,
则BCEVF-BCE=$\frac{1}{3}{S}_{△BCE}×EF$=$\frac{1}{3}×\frac{\sqrt{2}{a}^{2}}{2}×\frac{\sqrt{2}a}{2}$=$\frac{{a}^{3}}{6}$,
∴VM-BDP:VF-EBC=$\frac{1}{24}:\frac{1}{6}$=$\frac{1}{4}$.
点评 本题考查线面垂直的证明,考查两个三棱锥的体积之比的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
9.在六条棱长分别为2、3、3、4、5、5的所有四面体中,最大的体积是( )
| A. | $\frac{{8\sqrt{2}}}{3}$ | B. | $\frac{{5\sqrt{11}}}{6}$ | C. | $\frac{{\sqrt{462}}}{4}$ | D. | $2\sqrt{6}$ |
13.若存在两个正实数x,y,使得等式${x^3}{e^{\frac{y}{x}}}-a{y^3}=0$成立,其中e为自然对数的底数,则实数a的取值范围为( )
| A. | $[\frac{e^2}{8},+∞)$ | B. | $(0,\frac{e^3}{27}]$ | C. | $[\frac{e^3}{27},+∞)$ | D. | $(0,\frac{e^2}{8}]$ |
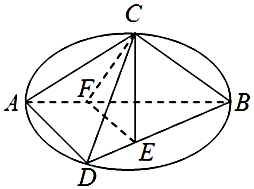 如图C,D是以AB为直径的圆上的两点,AB=2AD=2$\sqrt{3}$,AC=BC,F是AB上的一点,且AF=$\frac{1}{3}$AB,CE⊥面ABD,CE=$\sqrt{2}$.
如图C,D是以AB为直径的圆上的两点,AB=2AD=2$\sqrt{3}$,AC=BC,F是AB上的一点,且AF=$\frac{1}{3}$AB,CE⊥面ABD,CE=$\sqrt{2}$.