题目内容
18.已知函数f(x)=|x+1|+|x+m|.(1)若函数f(x)的最小值为2,求m的值;
(2)当x∈[-1,1]时,不等式f(x)≤2x+3恒成立,求m的取值范围.
分析 (1)求出f(x)的最小值,得到|m-1|=2,解出m的值即可;
(2)问题转化为-2x-2≤m≤2,即可求m的取值范围.
解答 解:(1)f(x)=|x+1|+|x+m|≥|(x+1)-(x+m)|=|m-1|,
当且仅当(x+1)(x+m)≤0时取等号,
∴f(x)min=|m-1|,
由|m-1|=2,解得:m=3或m=-1;
(2)当x∈[-1,1]时,不等式f(x)≤2x+3,即x+1+|x+m|≤2x+3,
∴-x-2≤x+m≤x+2,
∴-2x-2≤m≤2,
∵x∈[-1,1],
∴0≤m≤2.
点评 本题考查了解绝对值不等式问题,考查了等价转化的数学思想,是一道中档题.

练习册系列答案
相关题目
9.在六条棱长分别为2、3、3、4、5、5的所有四面体中,最大的体积是( )
| A. | $\frac{{8\sqrt{2}}}{3}$ | B. | $\frac{{5\sqrt{11}}}{6}$ | C. | $\frac{{\sqrt{462}}}{4}$ | D. | $2\sqrt{6}$ |
13.已知角α的终边过点P(-6,8),则cosα的值是( )
| A. | $-\frac{3}{5}$ | B. | $\frac{3}{5}$ | C. | $-\frac{4}{5}$ | D. | $\frac{4}{5}$ |
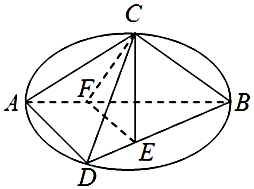 如图C,D是以AB为直径的圆上的两点,AB=2AD=2$\sqrt{3}$,AC=BC,F是AB上的一点,且AF=$\frac{1}{3}$AB,CE⊥面ABD,CE=$\sqrt{2}$.
如图C,D是以AB为直径的圆上的两点,AB=2AD=2$\sqrt{3}$,AC=BC,F是AB上的一点,且AF=$\frac{1}{3}$AB,CE⊥面ABD,CE=$\sqrt{2}$.