题目内容
(本小题满分14分)设椭圆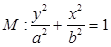 (
(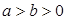 )经过点
)经过点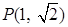 ,其离心率
,其离心率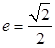 .
.
(Ⅰ)求椭圆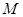 的方程;
的方程;
(Ⅱ) 直线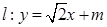 交椭圆于
交椭圆于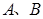 两点,且
两点,且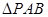 的面积为
的面积为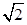 ,求
,求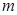 的值.
的值.
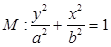 (
(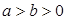 )经过点
)经过点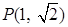 ,其离心率
,其离心率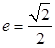 .
.(Ⅰ)求椭圆
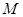 的方程;
的方程;(Ⅱ) 直线
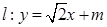 交椭圆于
交椭圆于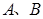 两点,且
两点,且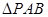 的面积为
的面积为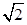 ,求
,求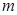 的值.
的值. (Ⅰ) (Ⅱ)
(Ⅱ)
 (Ⅱ)
(Ⅱ)
试题分析:(Ⅰ)由已知,得
 ,
,
 ,所求椭圆M的方程为
,所求椭圆M的方程为  .(6分)
.(6分)(Ⅱ)由
 ,得
,得 ,由
,由 得,
得, ,设
,设 ,
, ,
, .
. ∴


 .(9分)
.(9分)又
 到
到 的距离为
的距离为 .(10分)
.(10分)则
 ,
,所以
 ,
, ,
, ,
, ,
,显然
 ,故
,故 .(14分)
.(14分)点评:本题计算量较大,对于文科生是拉开差距的题目

练习册系列答案
相关题目
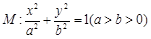 的离心率为
的离心率为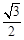 ,直线
,直线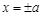 和
和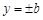 所围成的矩形ABCD的面积为8.
所围成的矩形ABCD的面积为8.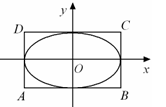
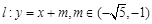 与椭圆M有两个不同的交点
与椭圆M有两个不同的交点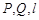 与矩形ABCD有两个不同的交点
与矩形ABCD有两个不同的交点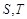 .求
.求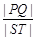 的最大值及取得最大值时m的值.
的最大值及取得最大值时m的值. 的中心在原点,焦点在
的中心在原点,焦点在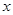 轴上,离心率为
轴上,离心率为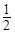 ,它的一个顶点恰好是抛物线
,它的一个顶点恰好是抛物线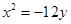 的焦点.
的焦点.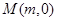 的直线
的直线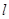 与椭圆
与椭圆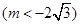 ,直线
,直线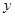 轴交于点
轴交于点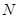 ,当
,当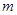 为何值时
为何值时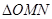 的面积有最小值?并求出最小值.
的面积有最小值?并求出最小值.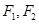 是椭圆
是椭圆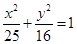 的两个焦点,点M在椭圆上,若△
的两个焦点,点M在椭圆上,若△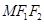 是直角三角形,则△
是直角三角形,则△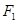 、
、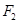 是椭圆
是椭圆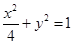 的左、右焦点,弦
的左、右焦点,弦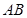 过
过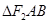 的周长为 .
的周长为 .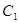 的离心率为
的离心率为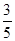 ,焦点在
,焦点在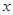 轴上,且长轴长为10,曲线
轴上,且长轴长为10,曲线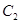 上的点与椭圆
上的点与椭圆 上一点
上一点 到焦点
到焦点 的距离为2,
的距离为2, 是
是 的中点,则
的中点,则 等于( )
等于( )


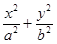 =1(a>b>o)的离心率e=
=1(a>b>o)的离心率e=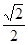 ,且经过点(
,且经过点(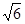 ,1),O为坐标原点。
,1),O为坐标原点。
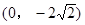 ,F2(0,
,F2(0,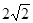 ),且离心率
),且离心率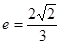 。
。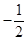 ,求直线l的斜率的取值范围。
,求直线l的斜率的取值范围。