题目内容
6.设p:实数t满足t2-5at+4a2<0(其中a≠0),q:方程$\frac{{x}^{2}}{t-2}$+$\frac{{y}^{2}}{t-6}$=1表示双曲线.(Ⅰ)若a=1,且p∧q为真命题,求实数t的取值范围;
(Ⅱ)若q是p的充分条件,求实数a的取值范围.
分析 (Ⅰ)若a=1,分别求出p,q成立的等价条件,利用p∧q为真命题,即可求实数t的取值范围;
(Ⅱ)利用q是p的充分条件,⇒命题q所包含的a的集合是命题p所包含a的集合的子集,求实数a的取值范围.
解答 解:(Ⅰ)命题p真:a=1,则不等式为t2-5t+4<0,即1<t<4,
命题q真:则(t-2)(t-6)<0,即2<t<6.
若p∧q为真命题,则p,q都为真命题,
即$\left\{\begin{array}{l}{1<t<4}\\{2<t<6}\end{array}\right.$,解得2<t<4,
则实数t的取值范围{t|2<t<4}.
(Ⅱ)命题p真:t2-5at+4a2<0(其中a≠0),则(t-a)(t-4a)<0,
若a>0,则得a<t<4a;若a<0,则4a<t<a,
q真:t∈(2,6),
∵若q是p的充分条件,
则当a>0时,$\left\{\begin{array}{l}{4a≥6}\\{a≤2}\end{array}\right.$⇒$\frac{3}{2}≤a≤2$;
若a<0,则不满足条件.
即实数a的取值范围是[$\frac{3}{2}$,2].
点评 本题主要考查复合命题与简单命题之间的关系,利用充分条件和必要条件的定义是解决本题的关键,属于基础题.

练习册系列答案
相关题目
14.已知扇形的半径为3,圆心角为$\frac{2π}{3}$,则扇形的弧长为( )
| A. | 3π | B. | 2π | C. | 360 | D. | 540 |
11.某几何体的三视图如图所示,则该几何体的体积为( )
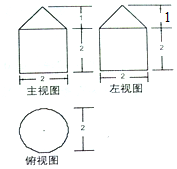

| A. | 2π | B. | $\frac{7}{3}$π | C. | $\frac{8}{3}$π | D. | 4π |
12.已知实数x,y满足$\left\{\begin{array}{l}2x-y+4≥0\\ x-2y-5≤0\\ x+2y-4≤0\end{array}\right.$,则z=2x+3y的最大值与最小值之差为( )
| A. | -$\frac{68}{3}$ | B. | $\frac{371}{12}$ | C. | $\frac{33}{4}$ | D. | $\frac{28}{5}$ |