题目内容

15．在△ABC中，关于x的方程（1+x2）sinA+2xsinB+（1-x2）sinC=0无实数根，则△ABC的形状为（　　）
A．锐角三角形B．钝角三角形C．直角三角形D．等边三角形

分析 先运用正弦定理，把角化为边，再将方程整理为一般式，再根据判别式的意义得到△=4b2-4（a-c）（a+c）＜0，即可判断三角形形状．

解答 解：由正弦定理，可得sinA=$\frac{a}{2R}$，sinB=$\frac{b}{2R}$，sinC=$\frac{c}{2R}$，
则关于x的方程（1+x2）sinA+2xsinB+（1-x2）sinC=0，
即为（1+x2）a+2xb+（1-x2）c=0
方程整理为（a-c）x2+2bx+a+c=0，
根据题意得△=4b2-4（a-c）（a+c）＜0，
∴a2＞b2+c2，
∴cosA＜0
∴A为钝角，
故选B．

点评 本题考查了一元二次方程ax2+bx+c=0（a≠0）的根的判别式△=b2-4ac：当△＞0，方程有两个不相等的实数根；当△=0，方程有两个相等的实数根；当△＜0，方程没有实数根．也考查了勾股定理的逆定理，属于中档题．

练习册系列答案
相关题目
8．我们常用函数y=f（x）的函数值的改变量与自变量的改变量的比值来表示平均变化率，当自变量x由x0改变到x+x0时，函数值的改变量△y等于（　　）
A．f（x0+△x）B．f（x0）+△xC．f（x0）•△xD．f（x0+△x）-f（x0）
9．已知变量x和y满足关系$\widehat{y}$=0.7x+0.35，变量y与z负相关，下列结论中正确的是（　　）
A．x与y正相关，x与z负相关B．x与y正相关，x与z正相关
C．x与y负相关，x与z负相关D．x与y负相关，x与z正相关
3．如图，约束条件为$\left\{\begin{array}{l}{y≤-\frac{1}{4}x+\frac{13}{4}}\\{y≥-x+4}\\{y≥\frac{1}{2}x-\frac{1}{2}}\end{array}\right.$，若在可行域△ABC上有无穷多个点（x，y），使得目标函数z=x+my取得最小值，求m的值．
10．点P在双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的右支上，其左、右焦点分别为F1，F2，直线PF1与以坐标原点O为圆心、a为半径的圆相切于点A，线段PF1的垂直平分线恰好过点F2，则该双曲线的渐近线的斜率为±$\frac{4}{3}$．
20．设函数f（x）=m（x+1）2ln（x+1）+[f′（e-1）-3e]x，其中x＞-1，曲线y=f（x）在点（0，0）处的切线方程为y=0
（Ⅰ）求f（x）的解析式
（Ⅱ）证明：当x≥0时，f（x）≥x2
（Ⅲ）若当x≥0时，f（x）≥ax2恒成立，求实数a的取值范围．
7．若${（1-2x）^{2017}}={a_0}+{a_1}x+{a_2}{x^2}+…+{a_{2017}}{x^{2017}}$，则（a0+a1）+（a0+a2）+…+（a0+a2017）=（　　）
A．2015B．2016C．2017D．2018
4．执行如图所示的程序框图，若输入的a=5，则输出的结果是（　　）
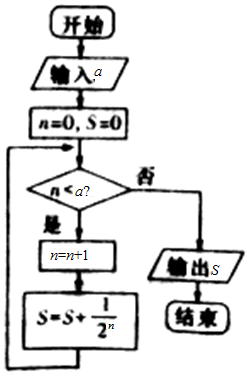
A．$\frac{15}{16}$B．$\frac{31}{16}$C．$\frac{31}{32}$D．$\frac{63}{32}$
5．已知函数$f（x）=\frac{ax}{lnx}$．
（1）若f（x）在点（e2，f（e2））处的切线与直线4x+y=0垂直，求函数f（x）的单调递增区间；
（2）若方程f（x）=1有两个不相等的实数解x1，x2，证明：x1+x2＞2e．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网