题目内容
三个数成等差数列,这三个数的和为26,三数之积为-24,求这三个数.
考点:等差数列的性质
专题:等差数列与等比数列
分析:设这三个数为a-d,a,a+d,由题意可得a和d的方程组,解方程组可得.
解答:
解:由题意设这三个数为a-d,a,a+d,
则
,
解得
或
,
∴所求三数为:-2,2,6或6,2,-2
则
|
解得
|
|
∴所求三数为:-2,2,6或6,2,-2
点评:本题考查等差数列和等比数列,巧妙设置未知量是解决问题的关键,属基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
函数y=f(x)满足:
①y=f(x+1)是偶函数;
②在[1,+∞)上为增函数.
则f(-1)与f(2)的大小关系是( )
①y=f(x+1)是偶函数;
②在[1,+∞)上为增函数.
则f(-1)与f(2)的大小关系是( )
| A、f(-1)>f(2) |
| B、f(-1)<f(2) |
| C、f(-1)=f(2) |
| D、无法确定 |
若“0≤x≤4”是“(x-a)[x-(a+2)]≤0”的必要不充分条件,则实数a的取值范围是( )
| A、(0,2) |
| B、[0,2] |
| C、[-2,0] |
| D、(-2,0) |
“x(x-3)<0”是“|x-1|<2”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
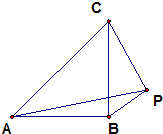 如图,在等腰直角△ABC中,∠ABC=90°,腰长为2,P为△ABC外一点,∠BPC=90°.
如图,在等腰直角△ABC中,∠ABC=90°,腰长为2,P为△ABC外一点,∠BPC=90°.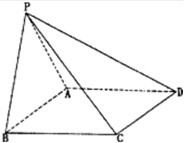 如图所示,四棱锥P-ABCD中,底面ABCD是菱形,∠ABC=60°,平面PAB⊥平面ABCD,PA=PB=AB.
如图所示,四棱锥P-ABCD中,底面ABCD是菱形,∠ABC=60°,平面PAB⊥平面ABCD,PA=PB=AB.