题目内容
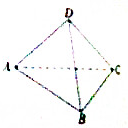 在空间四边形ABCD中,各边长均为a,对角线BD=
在空间四边形ABCD中,各边长均为a,对角线BD=| 2 |
考点:异面直线及其所成的角
专题:空间角
分析:取AC中点O,连结DO,BO,由已知得DO⊥AC,BO⊥AC,从而AC⊥平面BOD,由此能求出异面直线BD与AC所成的角为90°.
解答:
 解:∵在空间四边形ABCD中,各边长均为a,
解:∵在空间四边形ABCD中,各边长均为a,
∴AD=CD=AB=CB,
取AC中点O,连结DO,BO,
则DO⊥AC,BO⊥AC,
又DO∩BO=O,∴AC⊥平面BOD,
∵BD?平面BOD,∴AC⊥BD,
∴异面直线BD与AC所成的角为90°.
 解:∵在空间四边形ABCD中,各边长均为a,
解:∵在空间四边形ABCD中,各边长均为a,∴AD=CD=AB=CB,
取AC中点O,连结DO,BO,
则DO⊥AC,BO⊥AC,
又DO∩BO=O,∴AC⊥平面BOD,
∵BD?平面BOD,∴AC⊥BD,
∴异面直线BD与AC所成的角为90°.
点评:本题考查异面直线所成角的大小的求法,是中档题,解题时要注意空间思维能力的培养.

练习册系列答案
相关题目
三个数0.993.3,log3π,log20.8的大小关系为( )
| A、log3π<0.993.3<log20.8 |
| B、log20.8<log3π<0.993.3 |
| C、0.993.3<log20.8 l<og3π |
| D、log20.8<0.993.3<log3π |
已知A={2,lnx},B={x,y},A∩B={1},则实数x,y的值分别为( )
| A、e,0 | ||
| B、e,1 | ||
| C、1,e | ||
D、
|
已知全集U={1,3,5,7,9},A={1,5,7},则∁UA=( )
| A、{1,3} |
| B、{(3,9)} |
| C、{3,9} |
| D、{5,9} |
如果曲线C上任意一点的坐标都是方程F(x,y)=0的解,那么下列命题正确的是( )
| A、曲线C的方程是F(x,y)=0 |
| B、曲线C上的点都在方程F(x,y)=0的曲线上 |
| C、方程F(x,y)=0的曲线是C |
| D、以方程F(x,y)=0解为坐标点都在曲线C上 |
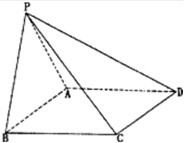 如图所示,四棱锥P-ABCD中,底面ABCD是菱形,∠ABC=60°,平面PAB⊥平面ABCD,PA=PB=AB.
如图所示,四棱锥P-ABCD中,底面ABCD是菱形,∠ABC=60°,平面PAB⊥平面ABCD,PA=PB=AB.