题目内容
本小题满分12分)在平行六面体 中,
中, ,
, ,
, 是
是 的中点.
的中点.

(1)证明: 面
面 ;
;
(2)若 ,求直线
,求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
(1)证明见解析;(2) .
.
【解析】
试题分析:(1)本题证明线面垂直,根据纯平面垂直的判定定理,只要证明直线 与平面
与平面 内的两条相交直线垂直即可,而从已知条件可看出只要在
内的两条相交直线垂直即可,而从已知条件可看出只要在 和
和 中利用正弦定理及勾股定理就能证得
中利用正弦定理及勾股定理就能证得 ,
, ;(2)本小题是求直线与平面所成的角,由(1)已经知道
;(2)本小题是求直线与平面所成的角,由(1)已经知道 ,
, ,再在
,再在 中应用勾股定理又可证明
中应用勾股定理又可证明 ,于是我们可以分别以
,于是我们可以分别以 为
为 轴建立窨直角坐标系,用向量法求解线面角.
轴建立窨直角坐标系,用向量法求解线面角.
试题解析:(1)证明:由 的中点
的中点 , 由
, 由 同理
同理
 平面
平面 .
.
(2) ,
,

 为直角三角形,
为直角三角形,
以 为原点,
为原点, 为
为 轴,
轴, 为
为 轴,
轴, 为
为 轴,建立坐标系,不妨设
轴,建立坐标系,不妨设 ,则
,则 ,
, ,
, ,
,
由
 ,
, 设
设 为平面
为平面 的法向量
的法向量
可求得


考点:1.线面垂直;2.直线与平面所成的角.

练习册系列答案
相关题目
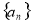 中,
中,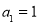 ,其前
,其前 项和
项和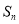 满足
满足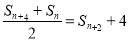 (
(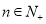 ).
).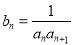 ,求数列
,求数列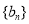 的前
的前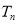 .
.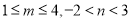 ,求
,求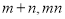 的取值范围;
的取值范围;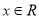 ,
,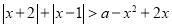 恒成立,求
恒成立,求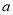 的取值范围.
的取值范围.
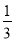 B.
B.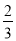 C.
C.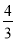 D.
D.
 ,求
,求 的取值范围;
的取值范围; ,
, 恒成立,求
恒成立,求 的取值范围.
的取值范围. 满足
满足 ,且
,且 ,则
,则 与
与 的夹角为 .
的夹角为 .
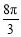 B.
B.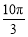 C.
C.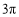 D.
D.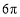
 ,
, ,则集合
,则集合 = .
= . 中,
中, ,
, ,
, ,则
,则 边上的高为( )
边上的高为( ) B.
B.
 D.
D.