题目内容
(本小题满分12分)已知等差数列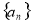 中,
中,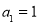 ,其前
,其前 项和
项和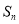 满足
满足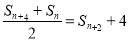 (
(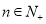 ).
).
(1)求数列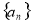 的通项公式;
的通项公式;
(2)令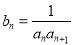 ,求数列
,求数列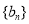 的前
的前 项和
项和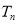 .
.
(1) ;(2)
;(2) .
.
【解析】
试题分析:(1)根据已知条件结合等差数列的性质,将条件中的式子转化为关于公差 的方程,求出公差
的方程,求出公差
 之后可进一步求出数列的通项公式;(2)根据(1)的结论,进一步可求出新数列的通项公式,最后采
之后可进一步求出数列的通项公式;(2)根据(1)的结论,进一步可求出新数列的通项公式,最后采
用裂项相消法求出数列的前 项和.
项和.
试题解析:(1)∵ ,∴
,∴ ,∴
,∴ ,
,
∴ , 2分
, 2分
∵数列 为等差数列,设公差为
为等差数列,设公差为 ,∴
,∴ ,即
,即 , 4分
, 4分
又∵ ,∴
,∴ ; 6分
; 6分
(2) , 9分
, 9分
∴
 . 12分
. 12分
考点:1.等差数列的通项公式及其前 项和;2.裂项相消求数列的和.
项和;2.裂项相消求数列的和.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
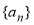 中,
中,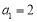 ,
,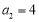 ,且
,且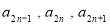 成等差数列,
成等差数列,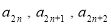 成等比数列,
成等比数列,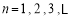 .
.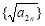 为等差数列;
为等差数列;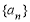 的通项公式.
的通项公式.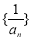 的前
的前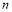 项和为
项和为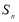 ,证明:
,证明: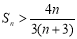 ,
,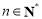 .
. ,
, ,全集
,全集 ,则
,则 ( )
( ) B.
B.
 D.
D.
 的图象沿
的图象沿 轴向右平移
轴向右平移 个单位后,得到一个偶函数的图象,则
个单位后,得到一个偶函数的图象,则 的取值不可能是( )
的取值不可能是( ) B.
B. C.
C. D.
D.
 是
是 的直径,
的直径, 是
是 为切点,
为切点, ,交
,交 ,连接
,连接 、
、 、
、 、
、 ,延长
,延长 交
交 于
于 .
.
 ;
; .
. 是定义在
是定义在 上周期为
上周期为 的函数,且对任意的实数
的函数,且对任意的实数 ,恒有
,恒有 ,当
,当 ,
, .若
.若 在
在 有且仅有三个零点,则
有且仅有三个零点,则 的取值范围为( )
的取值范围为( ) B.
B. C.
C. D.
D.
 中,
中, ,
, ,则数列
,则数列 项和
项和 ( )
( ) B.
B. C.
C. D.
D.
 上的函数
上的函数 ,当
,当 时,
时, ,且对于任意的实数
,且对于任意的实数 (
( ),都有
),都有 ,若函数
,若函数 有且只有三个零点,则
有且只有三个零点,则 的取值范围为( )
的取值范围为( ) B.
B. C.
C. D.
D.
 中,
中, ,
, ,
, 是
是 的中点.
的中点.
 面
面 ;
; ,求直线
,求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.