题目内容
(本小题满分10分)选修4-5:不等式选讲
(1)已知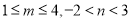 ,求
,求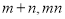 的取值范围;
的取值范围;
(2)若对任意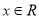 ,
,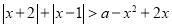 恒成立,求
恒成立,求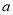 的取值范围.
的取值范围.
(1) (2)
(2) .
.
【解析】
试题分析:(1)本题考查不等式的基本性质,利用不等式的性质“不等式两边加上(或减去)同一个数(式),不等号的方向不变”的推论:“同向不等式相加,不改变不等号的方向”,可得出 的范围,由不等式的性质“不等式两边同乘以一个正数,不等号方向不变,同乘以一个负数,不等号的方向改变”可得推论:“
的范围,由不等式的性质“不等式两边同乘以一个正数,不等号方向不变,同乘以一个负数,不等号的方向改变”可得推论:“ ”,由此推论可求得
”,由此推论可求得 的范围,注意正负分类讨论;(2)本题属于不等式恒成立问题,我们采取参数分离法,变为
的范围,注意正负分类讨论;(2)本题属于不等式恒成立问题,我们采取参数分离法,变为 恒成立,从而只要求得
恒成立,从而只要求得 的最小值
的最小值 ,则有
,则有 .
.
试题解析:(1)由不等式的性质,由 得,
得, ,即
,即 ;
;
因为 ,当
,当 时,
时, ,则
,则 ,即
,即 ,∴
,∴ ,
,
当 时,
时, ,即
,即 ,所以
,所以 .
.
(2)对任意 ,
, 恒成立,变形为
恒成立,变形为 对任意
对任意 恒成立,由于
恒成立,由于 可表示数轴上点
可表示数轴上点 到-2和1两点的距离之和,因此当
到-2和1两点的距离之和,因此当 时,
时, 取得最小值3,
取得最小值3, ,所以当
,所以当 时,
时, 取得最小值-1,所以当
取得最小值-1,所以当 时,
时,

 取得最小值
取得最小值 ,所以
,所以 .
.
考点:1.不等式的性质;2.不等式恒成立问题;3.函数的最小值.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,
, ,全集
,全集 ,则
,则 ( )
( ) B.
B.
 D.
D.
 中,
中, ,
, ,则数列
,则数列 项和
项和 ( )
( ) B.
B. C.
C. D.
D.
 上的函数
上的函数 ,当
,当 时,
时, ,且对于任意的实数
,且对于任意的实数 (
( ),都有
),都有 ,若函数
,若函数 有且只有三个零点,则
有且只有三个零点,则 的取值范围为( )
的取值范围为( ) B.
B. C.
C. D.
D.
 的图象向左平移
的图象向左平移 个单位后得到
个单位后得到 的图象,则
的图象,则 的值为( )
的值为( ) B.
B. C.
C. D.
D.
 中,
中,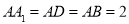 ,
,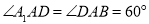 ,
,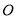 是
是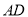 的中点.
的中点.
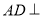 面
面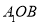 ;
;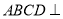 平面
平面 ,求
,求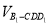 .
. ,若
,若 在
在 上恒成立,
上恒成立, 的取值范围是( )
的取值范围是( ) B.
B.  D.
D. 
 中,
中, ,
, ,
, 是
是 的中点.
的中点.
 面
面 ;
; ,求直线
,求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.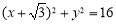 ,点
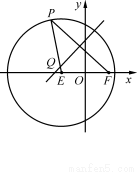
,点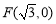 ,P是圆E上任意一点.线段PF的垂直平分线和半径PE相交于Q.
,P是圆E上任意一点.线段PF的垂直平分线和半径PE相交于Q.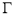 的方程;
的方程;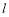 与(Ⅰ)中轨迹
与(Ⅰ)中轨迹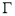 相交于
相交于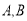 两点,直线
两点,直线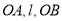 的斜率分别为
的斜率分别为 (其中
(其中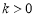 ).△
).△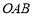 的面积为
的面积为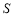 , 以
, 以 为直径的圆的面积分别为
为直径的圆的面积分别为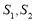 .若
.若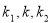 恰好构成等比数列, 求
恰好构成等比数列, 求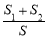 的取值范围.
的取值范围.