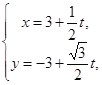Question

【题目】若函数f(x)和g(x)满足：①在区间[a，b]上均有定义；②函数y＝f(x)－g(x)在区间[a，b]上至少有一个零点，则称f(x)和g(x)在[a，b]上具有关系G．

（1）若f(x)＝lgx，g(x)＝3－x，试判断f(x)和g(x)在[1，4]上是否具有关系G，并说明理由；

（2）若f(x)＝2|x－2|＋1和g(x)＝mx2在[1，4]上具有关系G，求实数m的取值范围．

Answer 1

【答案】（1）具有关系G;（2）

【解析】试题分析：（1）利用零点存在定理可判断在区间 上至少有一个零点，即具有关系G;（2）先取绝对值，显然当时，无零点，当时， 时函数单调，如有零点则 ；最后讨论以及情况下， 是否有零点《结果无零点，因此可得

试题解析：（1）令 ，所以由区间根定理，函数在区间 上至少有一个零点，所以具有关系G;（2）当时， 函数在区间 上无零点，当时， ，所以当时， ；当时， ， 在区间 上无零点；当时， ， 在区间 上无零点，综上