题目内容
10.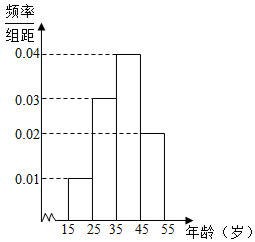 某游戏网站为了了解某款游戏玩家的年龄情况,现随机调查100位玩家的年龄整理后画出频率分布直方图如图所示.
某游戏网站为了了解某款游戏玩家的年龄情况,现随机调查100位玩家的年龄整理后画出频率分布直方图如图所示.(1)求100名玩家中各年龄组的人数,并利用所给的频率分布直方图估计该款游戏所有玩家的平均年龄;
(2)若已从年龄在[35,45),[45,55)的玩家中利用分层抽样选取6人组成一个游戏联盟,现从这6人中选出2人,求这两人在不同年龄组的概率.
分析 (Ⅰ)由直方图可得各组年龄的人数,由直方图计算平均值的方法可得平均年龄;
(Ⅱ)在[35,45)的人数为4人,记为a,b,c,d;在[45,55)的人数为2人,记为m,n.列举可得总的情况共有15种,“这两人在不同年龄组”包含8种,由古典概型概率公式可得.
解答 解:(Ⅰ)由直方图可得各组年龄的人数分别为10,30,40,20人;
估计所有玩家的平均年龄为0.1×20+0.3×30+0.4×40+0.2×50=37岁;
(Ⅱ)在[35,45)的人数为4人,记为a,b,c,d;在[45,55)的人数为2人,记为m,n.
∴抽取结果共有15种,列举如下:
(ab),(ac),(ad),(am),(an),(bc),(bd),(bm),(bn),(cd),
(cm),(cn),(dm),(dn),(mn)
设“这两人在不同年龄组”为事件A,事件A所包含的基本事件有8种,
则$P(A)=\frac{8}{15}$,∴这两人在不同年龄组的概率为$\frac{8}{15}$
点评 本题考查列举法计算基本事件数,涉及概率公式和直方图,列举是解决问题的关键,属中档题.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
18.执行如图所示的程序框图,则输出的k的值是( )


| A. | 10 | B. | 11 | C. | 12 | D. | 13 |
2.把一枚质地均匀的硬币连续抛2次,出现正、反面交替的概率是( )
| A. | $\frac{1}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{3}{8}$ | D. | $\frac{1}{2}$ |
20.若i是虚数单位,复数$z=\frac{i}{2+i}$的虚部为( )
| A. | $-\frac{1}{5}$ | B. | $-\frac{2}{5}$ | C. | $\frac{1}{5}$ | D. | $\frac{2}{5}$ |