题目内容
5.若数列{an}满足a1=-1,n(an+1-an)=2-an+1(n∈N*),则数列{an}的通项公式是an=2-$\frac{3}{n}$.分析 n(an+1-an)=2-an+1(n∈N*),化为(n+1)an+1-nan=2,利用等差数列的通项公式即可得出.
解答 解:∵n(an+1-an)=2-an+1(n∈N*),
∴(n+1)an+1-nan=2,
则数列{nan}是等差数列,首项为-1,公差为2.
∴nan=-1+2(n-1)=2n-3,
∴an=2-$\frac{3}{n}$.
故答案为:2-$\frac{3}{n}$.
点评 本题考查了等差数列的通项公式、递推关系,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
20.在等差数列{an}中,a3+a5=12-a7,则a1+a9=( )
| A. | 8 | B. | 12 | C. | 16 | D. | 20 |
17.在一次数学考试中,数学课代表将他们班50名同学的考试成绩按如下方式进行统计得到如下频数分布表(满分为100分)
(Ⅰ)在答题卡上作出这些数据中的频率分布直方图;
(Ⅱ)估计该班学生数学成绩的中位数和平均值;
(Ⅲ)若按照学生成绩在区间[0,60),[60,80),[80,100)内,分别认定为不及格,及格,优良三个等次,用分层抽样的方法从中抽取一个容量为5的样本,计算:从该样本中任意抽取2名学生,至少有一名学生成绩属于及格等次的概率.
| 成绩 | [40,50) | [50,60) | [60,70) | [70,80) | [80,90) | [90,100) |
| 人数 | 2 | 8 | 15 | 15 | 4 | 6 |
(Ⅱ)估计该班学生数学成绩的中位数和平均值;
(Ⅲ)若按照学生成绩在区间[0,60),[60,80),[80,100)内,分别认定为不及格,及格,优良三个等次,用分层抽样的方法从中抽取一个容量为5的样本,计算:从该样本中任意抽取2名学生,至少有一名学生成绩属于及格等次的概率.

15.某校组织由5名学生参加的演讲比赛,采用抽签法决定演讲顺序,在“学生A和B都不是第一个出场,B不是最后一个出场”的前提下,学生C第一个出场的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{5}$ | C. | $\frac{1}{9}$ | D. | $\frac{3}{20}$ |
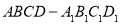 内接于半径为
内接于半径为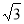 的半球
的半球 ,四边形
,四边形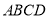 为正方形,则该四棱柱的体积最大时,
为正方形,则该四棱柱的体积最大时,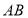 的长为( )
的长为( )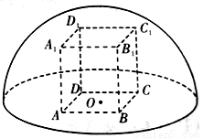
 B.
B.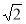 C.
C.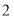
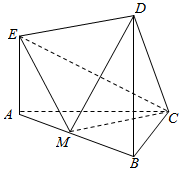 在如图所示的几何体中.EA⊥平面ABC,DB⊥平面ABC,AC⊥BC,且AC=BC=BD=2AE=2,M是AB的中点.
在如图所示的几何体中.EA⊥平面ABC,DB⊥平面ABC,AC⊥BC,且AC=BC=BD=2AE=2,M是AB的中点.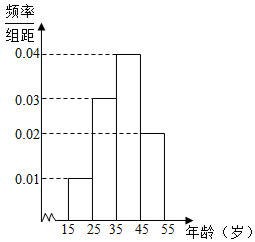 某游戏网站为了了解某款游戏玩家的年龄情况,现随机调查100位玩家的年龄整理后画出频率分布直方图如图所示.
某游戏网站为了了解某款游戏玩家的年龄情况,现随机调查100位玩家的年龄整理后画出频率分布直方图如图所示.