题目内容
1.集合A={(m,n)|(m+1)+(m+2)+…+(m+n)=61007,m∈Z,n∈N*},则集合A中的元素个数为2016.分析 由等差数列的前n和公式得出|(m+1)+(m+2)+…+(m+n)的和,问题转化为n(2m+n+1)=2×61007=21008•31007,讨论n与(n+2m+1)的可能取值多少种情况,从而求出集合A中的元素有多少.
解答 解:由(m+1)+(m+2)+…+(m+n)=$\frac{[(m+1)+(m+n)]•n}{2}$知,
n(2m+n+1)=2×61007=21008•31007;
又因为n,(n+2m+1)一奇一偶,
所以n是偶数时,n的取值为
21008,21008×3,21008×32,…,21008×31007,
共有1008个,交换顺序又得1008个;
所以,集合A中共有2016个元素.
故答案为:2016.
点评 本题考查了集合的概念与应用问题,也考查了等差数列求和与整数奇偶性的应用问题,是难题.

练习册系列答案
相关题目
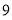 ,当其外接球的体积最小时, 它的高为( )
,当其外接球的体积最小时, 它的高为( )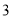 B.
B.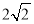 C.
C.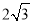 D.
D.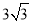
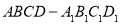 内接于半径为
内接于半径为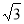 的半球
的半球 ,四边形
,四边形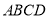 为正方形,则该四棱柱的体积最大时,
为正方形,则该四棱柱的体积最大时,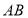 的长为( )
的长为( )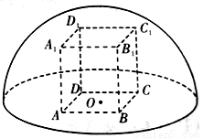
 B.
B.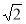 C.
C.
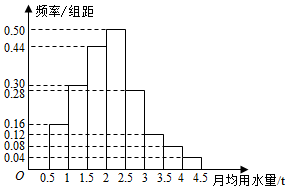
 在如图所示的几何体中.EA⊥平面ABC,DB⊥平面ABC,AC⊥BC,且AC=BC=BD=2AE=2,M是AB的中点.
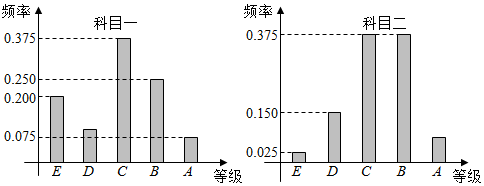
在如图所示的几何体中.EA⊥平面ABC,DB⊥平面ABC,AC⊥BC,且AC=BC=BD=2AE=2,M是AB的中点.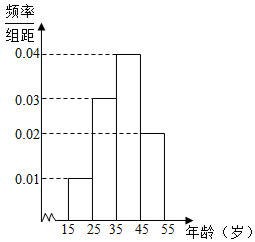 某游戏网站为了了解某款游戏玩家的年龄情况,现随机调查100位玩家的年龄整理后画出频率分布直方图如图所示.
某游戏网站为了了解某款游戏玩家的年龄情况,现随机调查100位玩家的年龄整理后画出频率分布直方图如图所示.