题目内容
2.把一枚质地均匀的硬币连续抛2次,出现正、反面交替的概率是( )| A. | $\frac{1}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{3}{8}$ | D. | $\frac{1}{2}$ |
分析 列举可得总的基本事件数和出现正、反面交替的基本事件数,由概率公式可得.
解答 解:把一枚质地均匀的硬币连续抛2次出现的结果为:
(正,正),(正,反),(反,正),(反,反)共4种情形,
其中出现正、反面交替的为:(正,反),(反,正)共2种情形,
故所求概率P=$\frac{2}{4}$=$\frac{1}{2}$
故选:D
点评 本题考查列举法计算基本事件数和事件发生的概率,属基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.在一次数学考试中,数学课代表将他们班50名同学的考试成绩按如下方式进行统计得到如下频数分布表(满分为100分)
(Ⅰ)在答题卡上作出这些数据中的频率分布直方图;
(Ⅱ)估计该班学生数学成绩的中位数和平均值;
(Ⅲ)若按照学生成绩在区间[0,60),[60,80),[80,100)内,分别认定为不及格,及格,优良三个等次,用分层抽样的方法从中抽取一个容量为5的样本,计算:从该样本中任意抽取2名学生,至少有一名学生成绩属于及格等次的概率.
| 成绩 | [40,50) | [50,60) | [60,70) | [70,80) | [80,90) | [90,100) |
| 人数 | 2 | 8 | 15 | 15 | 4 | 6 |
(Ⅱ)估计该班学生数学成绩的中位数和平均值;
(Ⅲ)若按照学生成绩在区间[0,60),[60,80),[80,100)内,分别认定为不及格,及格,优良三个等次,用分层抽样的方法从中抽取一个容量为5的样本,计算:从该样本中任意抽取2名学生,至少有一名学生成绩属于及格等次的概率.

12.已知集合A={x||x-a|<1},B={x|1<x<4},则A∪B=B,则实数a的取值范围是( )
| A. | [2,3] | B. | (2,3) | C. | [0,5] | D. | (0,5) |
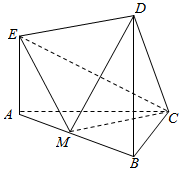 在如图所示的几何体中.EA⊥平面ABC,DB⊥平面ABC,AC⊥BC,且AC=BC=BD=2AE=2,M是AB的中点.
在如图所示的几何体中.EA⊥平面ABC,DB⊥平面ABC,AC⊥BC,且AC=BC=BD=2AE=2,M是AB的中点.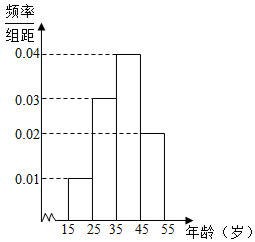 某游戏网站为了了解某款游戏玩家的年龄情况,现随机调查100位玩家的年龄整理后画出频率分布直方图如图所示.
某游戏网站为了了解某款游戏玩家的年龄情况,现随机调查100位玩家的年龄整理后画出频率分布直方图如图所示.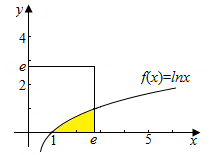 如图所示,若在边长为e(e为自然对数的底数)的正方形中随机撒一粒黄豆,则它落在阴影部分的概率为$\frac{1}{e^2}$.
如图所示,若在边长为e(e为自然对数的底数)的正方形中随机撒一粒黄豆,则它落在阴影部分的概率为$\frac{1}{e^2}$.