题目内容
已知双曲线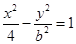 的右焦点与抛物线
的右焦点与抛物线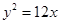 的焦点重合,则该双曲线的焦点到其渐近线的距离等于 .
的焦点重合,则该双曲线的焦点到其渐近线的距离等于 .
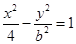 的右焦点与抛物线
的右焦点与抛物线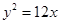 的焦点重合,则该双曲线的焦点到其渐近线的距离等于 .
的焦点重合,则该双曲线的焦点到其渐近线的距离等于 .
试题分析:因为抛物线的焦点为(3,0),所以
 ,因为双曲线的焦点到其渐近线的距离等于虚半轴长,所以应填
,因为双曲线的焦点到其渐近线的距离等于虚半轴长,所以应填 .
.点评:由抛物线的标准方程,可求出双曲线方程b的值,再根据双曲线的焦点到渐近线的距离等于虚半轴长b,问题得解.

练习册系列答案
相关题目
题目内容
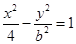 的右焦点与抛物线
的右焦点与抛物线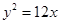 的焦点重合,则该双曲线的焦点到其渐近线的距离等于 .
的焦点重合,则该双曲线的焦点到其渐近线的距离等于 .
 ,因为双曲线的焦点到其渐近线的距离等于虚半轴长,所以应填
,因为双曲线的焦点到其渐近线的距离等于虚半轴长,所以应填 .
.