题目内容
已知椭圆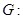
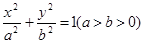 的离心率为
的离心率为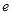 =
=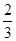 ,椭圆
,椭圆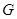 上的点
上的点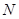 到两焦点的距离之和为12,点A、B分别是椭圆
到两焦点的距离之和为12,点A、B分别是椭圆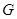 长轴的左、右端点,点F是椭圆的右焦点.点
长轴的左、右端点,点F是椭圆的右焦点.点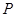 在椭圆上,且位于
在椭圆上,且位于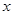 轴的上方,
轴的上方,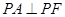 .
.
(I) 求椭圆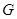 的方程;
的方程;
(II)求点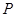 的坐标;
的坐标;
(III) 设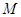 是椭圆长轴AB上的一点,
是椭圆长轴AB上的一点,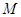 到直线AP的距离等于
到直线AP的距离等于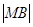 ,求椭圆上的点到点
,求椭圆上的点到点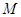 的距离
的距离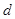 的最小值.
的最小值.
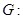
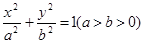 的离心率为
的离心率为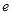 =
=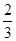 ,椭圆
,椭圆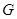 上的点
上的点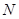 到两焦点的距离之和为12,点A、B分别是椭圆
到两焦点的距离之和为12,点A、B分别是椭圆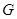 长轴的左、右端点,点F是椭圆的右焦点.点
长轴的左、右端点,点F是椭圆的右焦点.点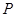 在椭圆上,且位于
在椭圆上,且位于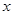 轴的上方,
轴的上方,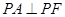 .
.(I) 求椭圆
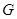 的方程;
的方程;(II)求点
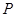 的坐标;
的坐标;(III) 设
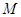 是椭圆长轴AB上的一点,
是椭圆长轴AB上的一点,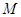 到直线AP的距离等于
到直线AP的距离等于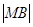 ,求椭圆上的点到点
,求椭圆上的点到点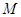 的距离
的距离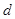 的最小值.
的最小值.解:(I)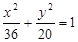 (II)点P的坐标是(
(II)点P的坐标是(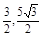 ) (III)当x=
) (III)当x=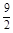 时,d取得最小值
时,d取得最小值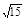 .
.
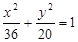 (II)点P的坐标是(
(II)点P的坐标是(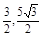 ) (III)当x=
) (III)当x=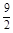 时,d取得最小值
时,d取得最小值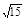 .
. 本试题主要是考查了椭圆方程的求解以及点的坐标的求解和圆锥曲线上点到点的距离的最值问题的求解的综合运用。
(1)因为椭圆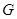 上的点
上的点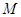 到两焦点的距离之和为12,
到两焦点的距离之和为12,
∴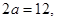
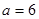 并且由离心率
并且由离心率 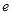 =
= ,∴
,∴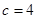
结合a,b,c关系,∴椭圆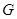 的方程为
的方程为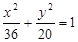
(2)由(1)可得点A(-6,0),B(6,0),F(0,4)
设点P(x,y),则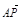 =(x+6,y),
=(x+6,y),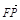 =(x-4,y),由已知可得联立方程组得到关于x的一元二次方程, 则 2x2+9x-18=0,x=
=(x-4,y),由已知可得联立方程组得到关于x的一元二次方程, 则 2x2+9x-18=0,x=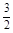 或x=-6.由于y>0,只能x=
或x=-6.由于y>0,只能x=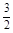 ,于是y=
,于是y=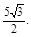
从而得到点P的坐标。
(3)直线AP的方程是x- +6=0
+6=0
设点M的坐标为(m,0),则M到直线AP的距离是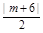 .
.
∴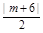 = |m-6|,又-6≤m≤6,解得m=2.
= |m-6|,又-6≤m≤6,解得m=2.
∴M点的坐标为(2,0)
设椭圆上的点(x,y)到点M的距离为d,则利用两点的距离公式可以解得最值
(1)因为椭圆
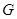 上的点
上的点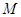 到两焦点的距离之和为12,
到两焦点的距离之和为12,∴
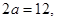
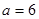 并且由离心率
并且由离心率 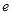 =
= ,∴
,∴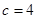
结合a,b,c关系,∴椭圆
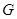 的方程为
的方程为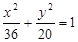
(2)由(1)可得点A(-6,0),B(6,0),F(0,4)
设点P(x,y),则
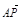 =(x+6,y),
=(x+6,y),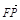 =(x-4,y),由已知可得联立方程组得到关于x的一元二次方程, 则 2x2+9x-18=0,x=
=(x-4,y),由已知可得联立方程组得到关于x的一元二次方程, 则 2x2+9x-18=0,x=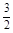 或x=-6.由于y>0,只能x=
或x=-6.由于y>0,只能x=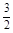 ,于是y=
,于是y=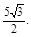
从而得到点P的坐标。
(3)直线AP的方程是x-
 +6=0
+6=0 设点M的坐标为(m,0),则M到直线AP的距离是
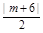 .
.∴
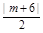 = |m-6|,又-6≤m≤6,解得m=2.
= |m-6|,又-6≤m≤6,解得m=2. ∴M点的坐标为(2,0)
设椭圆上的点(x,y)到点M的距离为d,则利用两点的距离公式可以解得最值

练习册系列答案
相关题目
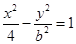 的右焦点与抛物线
的右焦点与抛物线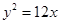 的焦点重合,则该双曲线的焦点到其渐近线的距离等于 .
的焦点重合,则该双曲线的焦点到其渐近线的距离等于 .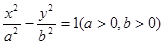 的左、右焦点分别为F1,F2,若在双曲线的右支上存在一点P,使得|PF1|=3|PF2|,则双曲线的离心率e的取值范围为 .
的左、右焦点分别为F1,F2,若在双曲线的右支上存在一点P,使得|PF1|=3|PF2|,则双曲线的离心率e的取值范围为 . 为原点,双曲线
为原点,双曲线 上有一点
上有一点 ,过
,过 ,平行四边形
,平行四边形 的面积为1,则双曲线的离心率为( )
的面积为1,则双曲线的离心率为( )



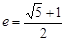 的双曲线
的双曲线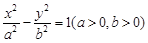 称为黄金双曲线.如图(图2)给出以下几个说法:
称为黄金双曲线.如图(图2)给出以下几个说法:
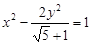 是黄金双曲线; ②若
是黄金双曲线; ②若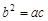 ,则该双曲线是黄金双曲线;
,则该双曲线是黄金双曲线;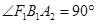 ,则该双曲线是黄金双曲线;④若
,则该双曲线是黄金双曲线;④若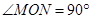 ,则该双曲线是黄金双曲线.其中正确的是
,则该双曲线是黄金双曲线.其中正确的是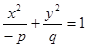 表示双曲线,则下列椭圆中,与该双曲线共焦点的是( )
表示双曲线,则下列椭圆中,与该双曲线共焦点的是( )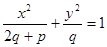
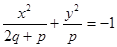
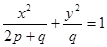
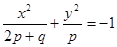
 是以
是以 为焦点的抛物线
为焦点的抛物线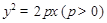 ,
, 是以直线
是以直线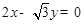 与
与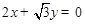 为渐近线,以
为渐近线,以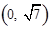 为一个焦点的双曲线.
为一个焦点的双曲线.
 和
和 ,求
,求 的取值范围,并求
的取值范围,并求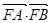 的最大值;(3)若
的最大值;(3)若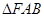 的面积
的面积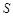 满足
满足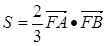 ,求
,求 (
( )的左、右焦点分别为
)的左、右焦点分别为 ,
, 为双曲线右支上一点,
为双曲线右支上一点, 与圆
与圆 切于点
切于点 ,且
,且 ,则它的离心率为______.
,则它的离心率为______.