题目内容
设A(x1，y1)，B(x2，y2)是椭圆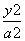
＋
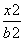＝1(a>b>0)上的两点
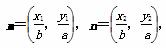，且
m·n＝0，椭圆离心率e＝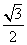
，短轴长为2，O为坐标原点．
(1)求椭圆方程；
(2)若存在斜率为k的直线AB过椭圆的焦点F(0，c)(c为半焦距)，求k的值．
解：(1)由
，解得a＝2，b＝1.
∴所求椭圆方程为
＋x2＝1.
(2)设直线AB的方程为y＝kx＋
.
由
⇒(k2＋4)x2＋2kx－1＝0，
＝x1x2＋
(kx1＋)(kx2＋)
＝
＝0.
解得k＝±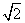
.
练习册系列答案
相关题目
＝0上点P作圆x2＋y2＝1的两条切线，若两条切线的夹角是60°，则点P的坐标是________．
，则点P的轨迹为( )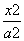
＋
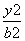＝1(a＞b＞0)的焦点垂直于x轴的弦长为
a，则双曲线
B.
D.
中，下列几种说法正确的是( ) 
B．
与
成
角 D．
与
成
角
，集合
，
，则
=（ ）
B．
C. 
D．